26-11-2020 door: Daan Veraart
Belofte maakt schuld. Zo ook mijn belofte onderaan mijn vorige blog om een neuraal netwerk te bouwen in Excel. Of om iets preciezer te zijn, een kunstmatig neuraal netwerk. Want een neuraal netwerk dankt zijn naam de neuron, een cel uit het menselijk lichaam die wordt gezien als de kern van menselijke intelligentie. In een super versimpelde versie werkt een neuron als volgt: Er komt een prikkel binnen in de neuron en als deze prikkel sterk genoeg is dan geeft de neuron een prikkel door aan andere neuronen en als je maar genoeg van die neuronen hebt (stuk of 100 miljard) heb je menselijke intelligentie.
Natuurlijk is het wel iets ingewikkelder dan dat, maar ik moet in dit blog ook nog 2-waarde logica uitleggen, een vage referentie maken naar 3-waarden logica, inconsistent zijn over of het waarde of waarden logica is, uitleggen hoe een heel basic kunstmatig neuraal netwerk werkt en klagen over dat ik mijn zinnen niet te lang mag maken en onder de 1000 woorden moet proberen te blijven, dus we laten het daar voorlopig even bij.
Want om de werking van een neuraal netwerk uit te leggen is het leuk om hem iets te leren en aangezien ik 3 waarden logica nog een keer zou uitleggen is het geen slecht idee om te beginnen met 2 waarden logica. De basis van 2 waarden logica is heel simpel. Iets is waar of iets is onwaar. Bijvoorbeeld: Je bent ouder dan 50. Dat is waar of onwaar. Als je twee statements hebt dan kan je die met een operator samenvoegen. Bijvoorbeeld: Je bent ouder dan 50 en je bent binnen 6 maanden jarig. De operator (in dit geval ‘en’) heeft van de 2 stellingen 1 stelling gemaakt waarbij de operator aangeeft hoe je aan de individuele stellingen moet voldoen om aan de gehele stelling te voldoen. Om het wat inzichtelijker te maken heb je in de logica waarheidstafels. Die zien er bijvoorbeeld zo uit:
| A | B | A en B |
| Waar | Waar | Waar |
| Waar | Onwaar | Onwaar |
| Onwaar | Waar | Onwaar |
| Onwaar | Onwaar | Onwaar |
Dat is de waarheidstafel voor ‘en’, we kunnen daar ook andere operators bijzetten zoals ‘of’, ‘niet en’, ‘niet of’ en ‘exof’. Laat ik ze eerst invullen, leg ik ze daarna verder uit.
| A | B | A en B | A of B | Niet (A en B) | Niet (A of B) | A exof B | Niet(A exof B) |
| Waar | Waar | Waar | Waar | Onwaar | Onwaar | Onwaar | Waar |
| Waar | Onwaar | Onwaar | Waar | Waar | Onwaar | Waar | Onwaar |
| Onwaar | Waar | Onwaar | Waar | Waar | Onwaar | Waar | Onwaar |
| Onwaar | Onwaar | Onwaar | Onwaar | Waar | Waar | Onwaar | Waar |
Ik denk dat het meeste wel voor zich spreekt. Exof is niet een heel gangbare term dus die zal ik nog even toelichten. Exof is de Nederlandse vertaling van xor (de veel bekendere term) en de afkorting voor ‘exclusieve of’. Het is eigenlijk hoe we vaak in de spreektaal ‘of’ gebruiken. Het is A of B, maar niet allebei. Hoewel die exclusiviteit in de spreektaal wordt geïmpliceerd is hij er technisch gezien niet, dus is ‘ja’ of ‘nee’ een valide antwoord op een ‘of’ vraag (daar is zelfs een subreddit voor), maar je bereikt er vaak niet veel meer mee dan dat iemand met zijn ogen rolt.
Nou klinken dit misschien als hele triviale dingen die logica operatoren, maar ze vormen wel de kern van moderne computers, hetgeen dit spel bijvoorbeeld laat zien. Maar in dat geval zijn deze zogenaamde logic-gates ingebakken in je computer, we gaan nu proberen Excel ze te laten leren. Dat gaan we doen met een neuraal netwerk, daarvoor moet ik nog wel even de basis van een neuraal netwerk uitleggen. Ons netwerk heeft 2 input neuronen (A en B uit de waarheidstafels) en 1 output neuron die aangeeft of bij de gegeven input de operatie waar is. Ons neurale netwerk ziet er zo uit:
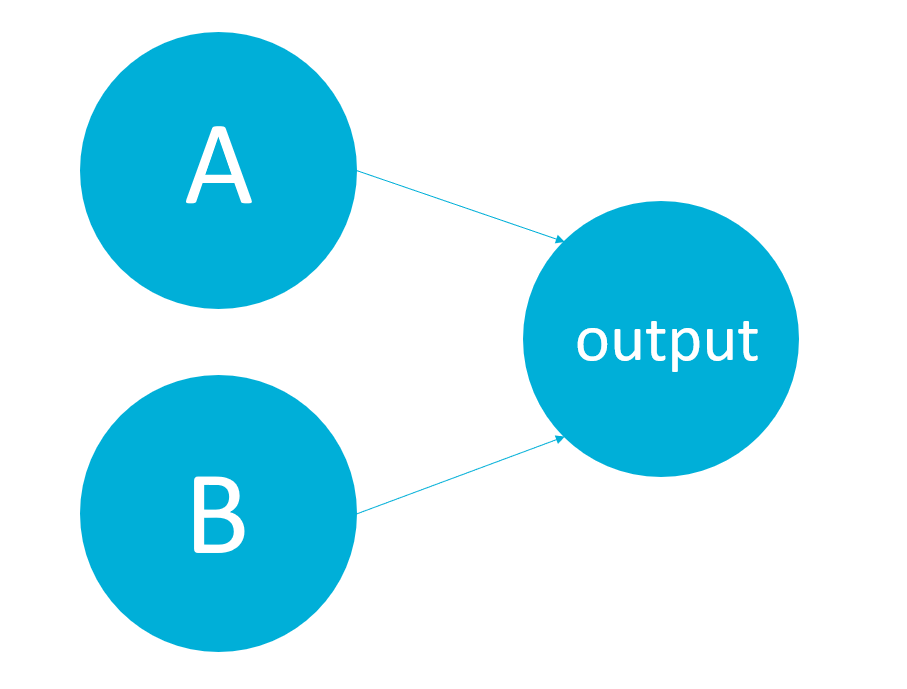
Veel simpeler dan dat worden neurale netwerken niet. Google maar eens op afbeeldingen van neurale netwerken, ze hebben allemaal veel meer neuronen en meer lagen, maar die ga ik niet allemaal in Excel programmeren en we hebben er ook niet meer nodig (eigenlijk wel, maar dat komt pas later.)
In het neurale netwerk krijgen A en B de waardes waar of onwaar. Dat representeren we als 1 voor waar en 0 voor onwaar (dat rekent een stuk makkelijker dan tekst). De verbindingen van A en B naar de output neuron hebben een gewicht. Dat zorgt er voor dat A en B niet even zwaar hoeven mee te wegen voor de beslissing. Als de verbinding van A een gewicht heeft van 0.2 en die van B 0.7 dan betekent dat als A waar is (dus 1) de output neuron de waarde heeft van 0.2. Als B aanstaat 0.7, en als ze allebei aanstaan 0.9.
Een waarde van 0.2 zegt in ons geval niet zoveel, iets kon waar zijn (1) of onwaar (0), wat 0.2 is weten we niet, daarom krijgt de output neuron een zogenaamde ‘actiepotentiaal grenswaarde’. Dat is de waarde die in ons supersimpele neuron uitleg bepaalt of het signaal doorgestuurd moet worden of niet. Komt de waarde van het signaal dat binnen komt boven deze waarde dan is de uitkomst 1 anders is deze 0. Stel we zetten de grenswaarde in ons voorbeeld op 0.6 dan gaat deze af zodra B waar is en maakt het eigenlijk niet uit of A wel of niet waar is. Hetgeen je zou kunnen schrijven met operatoren als: (A of niet A) en B. Of simpeler als: B. Willen we de ‘en’ operator simuleren dan moet de grenswaarde hoger liggen bijvoorbeeld op 0.8 want dan zijn opgeteld A en B genoeg om boven die waarde te komen. Voor ‘of’ moet hij een stuk lager liggen, bijvoorbeeld 0.1.
Maar hoe kan het netwerk deze waardes nou zelf leren? Daarvoor gebruiken we een versimpelde versie van een strategie met de naam backpropagation. Het idee is dat je het netwerk in het begin willekeurige waardes geeft voor de gewichten en grenswaarde(s) en dan vervolgens de uitkomsten dat het geeft gaat beoordelen, is het goed? Prima, niets aan doen, is het fout, dan moeten de waardes aangepast worden. Je begint hierbij aan het einde van het netwerk en werkt je weg terug. Dat is voor ons gelukkig een hele korte reis.
Als de uitkomst van het netwerk niet overeenkomt met het goede antwoord, dan passen we de actiepotentiaalgrenswaarde aan, dacht het netwerk 1 en was het 0, gaat de waarde omhoog, want we willen voorkomen dat hij bij de binnengekomen waarde afgaat en daarvoor moet je zorgen dat de grenswaarde boven de input waarde ligt, dat doet hij nu duidelijk nog niet. Omgekeerd als het netwerk 0 gokt en het had 1 moeten zijn gaat de grenswaarde naar beneden. Voor de wegingen van A en B naar de output neuron passen we de waarde willekeurig naar boven of beneden aan. Dat is niet de mooiste oplossing, maar ik wil niet te veel intelligentie in de foutcode stoppen voor een dergelijk simpel netwerk, dat voelt als valsspelen.
De Excel staat hier ik heb de functies EN, OF en NEN gemaakt, als je wilt kan je zelf NOF er ook nog inbouwen. Het gaat afhankelijk van de startwaardes en een beetje mazzel goed voor deze 3 operatoren. Ik laat het als huiswerkopdracht (ik ben al weer ruim over de 1000 woorden heen) waarom dit netwerk te klein is voor de EXOF. Kom je daar echt niet uit moet je maar een mailtje sturen of aanschieten op LinkedIn.