10-02-2017 door: Daan Veraart
Vaak als ik tegen mensen zeg dat ik programmeer voor mijn werk, krijg ik direct de vraag: “Is dat niet heel moeilijk?”. Volledig politiek verantwoord zeg ik dan dat het wel meevalt en dat zij misschien niet kunnen programmeren, maar dat ik dan weer helemaal geen verstand heb van hun werk. Dat is niet helemaal waar, ik heb meestal best wel veel verstand van wat voor werk ze dan ook mogen doen, maar je wilt niet te arrogant overkomen, dus je vlakt het allemaal wat af. Maar zonder gekheid, qua moeilijkheidsgraad is programmeren goed te vergelijken met schilderen, als je het plafond van de sixtijnse kapel moet schilderen, ja dat is niet makkelijk. Als het echter één groot blauw vlak moet worden, dat is prima te doen. Nu kan het tweede technisch gezien misschien wel geen schilderen, maar verven zijn, of sauzen, maar van schilderen heb ik geen verstand.
Wat programmeren vaak lastig maakt, is dat je programma met alle mogelijke scenario’s om moet kunnen gaan. Hoe meer verschillende mogelijkheden er zijn, hoe moeilijker het is om te maken. De truc is dan ook om zoveel mogelijk te anticiperen, wat kan er gebeuren en wat moet het programma dan doen? Ik zal dit proberen toe te lichten met een voorbeeld. Ik ga proberen het makkelijk te houden, zodat ook iedereen zonder programmeer kennis het kunnen volgen, maar mocht je meer uitleg willen mag je me altijd mailen.
Stel, je wilt de volgende wiskundige stelling bewijzen: y*x = y / (1/x) (Wat zoveel betekend als: getal A keer getal B is het zelfde als getal A gedeeld door 1 gedeeld door getal B, Bijvoorbeeld: 2*4 = 8 = 2/¼ (mocht je de wiskunde niet volgen, verlies niet de moed, het is voor de rest van het voorbeeld niet perse nodig). Mensen die goed zijn in wiskunde zullen direct zien dat die stelling klopt. Mensen die heel goed zijn in wiskunde zien dat die stelling klopt, behalve als x gelijk is aan nul, want je kunt immers niet delen door nul.
Dat is dan ook iets waar je in je programma rekening mee moet houden, wat als X nul is, of wat als het null is? Nu moet ik natuurlijk eerst uitleggen wat het verschil tussen nul en null is. Misschien is het toch allemaal niet zo makkelijk als ik dacht, maar we geven niet op! Voor wiskundige is 0 hetzelfde als niets, voor een computer is een 0 een getal en null het ontbreken van data. Ik zal een voorbeeld geven, neem de volgende tabel met vollédig verzonnen en willekeurige data:
| medewerker | blogs |
| Jurrie | 1 |
| Michael | 2 |
| Sjaak | 2 |
| Peter | 1 |
| Patrick | 7 |
| Kees | 13 |
| Bert | 0 |
| Manfred | 0 |
| Katinka | 0 |
| Wouter V | 1 |
| Bonneke | 0 |
| Bart | 0 |
| Daan | 0 |
| Marlies | 1 |
| Liesbeth | 0 |
| Wouter B | 0 |
Als je aan de computer vraagt hoeveel blogs heeft Daan geplaatst, dan is het antwoord 0. Als je vraagt hoeveel blogs heeft Aaron geplaatst dan is het antwoord null. Hij heeft namelijk de naam Aaron niet in de tabel staan, heeft dus niks om terug te geven en geeft dan het antwoord null, hoe de programmeertaal daarmee omgaat wisselt dan vervolgens ook weer.
Terug naar het voorbeeld, we hebben de volgende som: Y / (1 / X ). Voor het voorbeeld nemen we voor Y = 2, en voor X = 4 of 0 of null, en bekijken wat voor resultaat dat geeft. Voor wie wel kan programmeren, ik ga het in 3 talen doen: SQL (in een Oracle database), javascript (in de Chrome console) en haskell (via tryhaskell.org), probeer de uitkomsten eens te voorspellen. Voor als je niet kunt programmeren negeer de code waarmee het resultaat wordt berekend, het gaat nu even alleen om het resultaat.
Eerst in SQL:
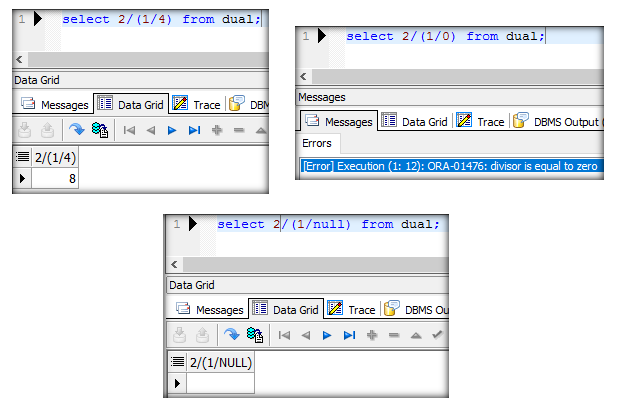
Zoals verwacht geeft de eerste berekening, 2 gedeeld door een kwart, het antwoord 8, normale situaties zijn gelukkig vaak makkelijk te voorspellen. Het tweede scenario, 2/ (1/0) geeft een foutmelding: “de deler is gelijk aan 0”. Ook dat was te verwachten, immer kan je volgens de wiskunde niet delen door 0. De laatste optie, 2/(1/null) geeft geen foutmelding, maar null (in sql wordt dit weergegeven door een leeg waarde. Dat betekend dus dat als je een berekening hebt met een deling, dat je altijd moet bedenken: wat moet mijn programma doen als de deler 0 is, en wat als de deler null is? Want een foutmelding of niks, is vaak niet wat je de gebruiker wilt laten zien.
Laten we eens kijken hoe hetzelfde werkt in Javascript:
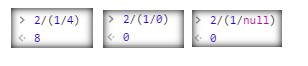
De eerste waarde is weer 8, zoals ik al zei zijn normale situaties gelukkig vaak makkelijk te voorspellen. Bij de twee volgende scenario’s krijgen we alleen andere resultaten, het antwoord is niet een foutmelding of een lege waarde, maar het getal 0.
Dan Haskell:

Bij Haskell zijn de eerste 2 het zelfde als bij JavaScript, de laatste is misschien een beetje oneerlijk, Haskell is een computertaal die eigenlijk geen null waarde kent, dat heeft te maken met het feit dat het een functionele programmeertaal is en geen variabele kent, maar dat leg ik misschien een andere keer nog wel uit. Om het na te bootsen haal ik hier de 3de waarde uit een lijst met 2 waardes, waarop ik de foutmelding “index is too large” terug krijg, als ik hetzelfde grapje in JavaScript uit haal krijg ik geen foutmelding maar “undefined” terug, SQL geeft ook geen foutmelding, maar helemaal niks (ook geen null dus). Bij Haskell hoef je er dus geen rekening mee houden dat er door null gedeeld kan worden, het kent namelijk geen null. Wel moet je bedenken wat je doet als iemand het toch probeert.
Het was een heel verhaal, maar uit dit voorbeeld blijkt dus dat je bij een deling altijd moet oppassen voor nul en null waardes. Want het is iets wat eigenlijk niet zou mogen gebeuren, en kan leiden tot onverwachte resultaten. Hetzelfde geldt ook voor het gebruik van de modulo functie (mocht je die niet kennen verwijs ik je naar wikipedia, anders wordt dit stuk veel te lang) en de wortel van een getal, 0 geeft foutmeldingen of onverwachte antwoorden.
Nou vooruit we maken het nog íets ingewikkelder. In Javascript en Haskell is 2/(1/0) = 0. Maar als we dat weten, wat is dan 1/0? Beide talen geven gelukkig weer hetzelfde antwoord:

Om je uit te kunnen leggen waarom dat ‘klopt’ moet ik je het idee van het drijvendekommagetal gaan uitleggen, en hoewel dat een topscrabblewoord is, lijkt het me voor wat ik probeer uit te leggen niet echt zinvol, dus neem van mij aan, dat ‘klopt’. Het verklaart overigens wel mooi waarom we het resultaat 2/(1/0) = 0 krijgen, Wat je eigenlijk doet is dus 2/Infinity en dat is dan weer 0, tenminste zolang je dat niet met een wiskundige overlegt kom je daar wel mee weg. Wat ook nog wel leuk is, in Haskell kan je ook delen met de div functie, dat geeft het volgende resultaat:

Daar moet je dan wel weer rekening mee houden. Kort samengevat, programmeren is niet moeilijk zolang je alle mogelijke scenario’s en gebruikersinvoer weet te voorspellen. Gelukkig zijn er testers, die proberen alle scenario’s die zij kunnen bedenken, en testen die uit. Dat vangt vaak het grootste gedeelte wel af.
Gelukkig heeft dit verhaal ook een gouden randje. De volgende keer dat je een programma hebt dat vastloopt of een verkeerd resultaat geeft, realiseer je dan, dat jij iets hebt gedaan dat zo origineel en vindingrijk was, dat de programmeur het van tevoren niet kon bedenken! Dus hoe vaker je computer vastloopt hoe fantasievoller/vindingrijker/inventiever jij bent!
Nou vooruit, om het nog nét iets ingewikkelder te maken. Met de round functie kun je getallen afronden. Dus round(1,2) = 1 en round(1,9) = 2. Probeer eens te voorspellen wat gebeurt er als we 1/0 afronden in Javascript en in Haskell.
Klik hier voor het antwoord
Ik had afgesproken dat ik het simpel zou houden geloof ik, ik denk dat ik het dan hierbij maar laat, want ik voorzie dat dit allemaal toch nog wel wat vragen op gaat leveren.
O rest me nog 1 dingetje:update orcado_blogs
set blogs = 1
where medewerker = 'Daan';
commit;
We moeten onze fictieve data wel integer houden.