Belofte maakt schuld. Zo ook mijn belofte onderaan mijn vorige blog om een neuraal netwerk te bouwen in Excel. Of om iets preciezer te zijn, een kunstmatig neuraal netwerk. Want een neuraal netwerk dankt zijn naam de neuron, een cel uit het menselijk lichaam die wordt gezien als de kern van menselijke intelligentie. In een super versimpelde versie werkt een neuron als volgt: Er komt een prikkel binnen in de neuron en als deze prikkel sterk genoeg is dan geeft de neuron een prikkel door aan andere neuronen en als je maar genoeg van die neuronen hebt (stuk of 100 miljard) heb je menselijke intelligentie.
Natuurlijk is het wel iets ingewikkelder dan dat, maar ik moet in dit blog ook nog 2-waarde logica uitleggen, een vage referentie maken naar 3-waarden logica, inconsistent zijn over of het waarde of waarden logica is, uitleggen hoe een heel basic kunstmatig neuraal netwerk werkt en klagen over dat ik mijn zinnen niet te lang mag maken en onder de 1000 woorden moet proberen te blijven, dus we laten het daar voorlopig even bij.
Want om de werking van een neuraal netwerk uit te leggen is het leuk om hem iets te leren en aangezien ik 3 waarden logica nog een keer zou uitleggen is het geen slecht idee om te beginnen met 2 waarden logica. De basis van 2 waarden logica is heel simpel. Iets is waar of iets is onwaar. Bijvoorbeeld: Je bent ouder dan 50. Dat is waar of onwaar. Als je twee statements hebt dan kan je die met een operator samenvoegen. Bijvoorbeeld: Je bent ouder dan 50 en je bent binnen 6 maanden jarig. De operator (in dit geval ‘en’) heeft van de 2 stellingen 1 stelling gemaakt waarbij de operator aangeeft hoe je aan de individuele stellingen moet voldoen om aan de gehele stelling te voldoen. Om het wat inzichtelijker te maken heb je in de logica waarheidstafels. Die zien er bijvoorbeeld zo uit:
| A | B | A en B |
| Waar | Waar | Waar |
| Waar | Onwaar | Onwaar |
| Onwaar | Waar | Onwaar |
| Onwaar | Onwaar | Onwaar |
Dat is de waarheidstafel voor ‘en’, we kunnen daar ook andere operators bijzetten zoals ‘of’, ‘niet en’, ‘niet of’ en ‘exof’. Laat ik ze eerst invullen, leg ik ze daarna verder uit.
| A | B | A en B | A of B | Niet (A en B) | Niet (A of B) | A exof B | Niet(A exof B) |
| Waar | Waar | Waar | Waar | Onwaar | Onwaar | Onwaar | Waar |
| Waar | Onwaar | Onwaar | Waar | Waar | Onwaar | Waar | Onwaar |
| Onwaar | Waar | Onwaar | Waar | Waar | Onwaar | Waar | Onwaar |
| Onwaar | Onwaar | Onwaar | Onwaar | Waar | Waar | Onwaar | Waar |
Ik denk dat het meeste wel voor zich spreekt. Exof is niet een heel gangbare term dus die zal ik nog even toelichten. Exof is de Nederlandse vertaling van xor (de veel bekendere term) en de afkorting voor ‘exclusieve of’. Het is eigenlijk hoe we vaak in de spreektaal ‘of’ gebruiken. Het is A of B, maar niet allebei. Hoewel die exclusiviteit in de spreektaal wordt geïmpliceerd is hij er technisch gezien niet, dus is ‘ja’ of ‘nee’ een valide antwoord op een ‘of’ vraag (daar is zelfs een subreddit voor), maar je bereikt er vaak niet veel meer mee dan dat iemand met zijn ogen rolt.
Nou klinken dit misschien als hele triviale dingen die logica operatoren, maar ze vormen wel de kern van moderne computers, hetgeen dit spel bijvoorbeeld laat zien. Maar in dat geval zijn deze zogenaamde logic-gates ingebakken in je computer, we gaan nu proberen Excel ze te laten leren. Dat gaan we doen met een neuraal netwerk, daarvoor moet ik nog wel even de basis van een neuraal netwerk uitleggen. Ons netwerk heeft 2 input neuronen (A en B uit de waarheidstafels) en 1 output neuron die aangeeft of bij de gegeven input de operatie waar is. Ons neurale netwerk ziet er zo uit:
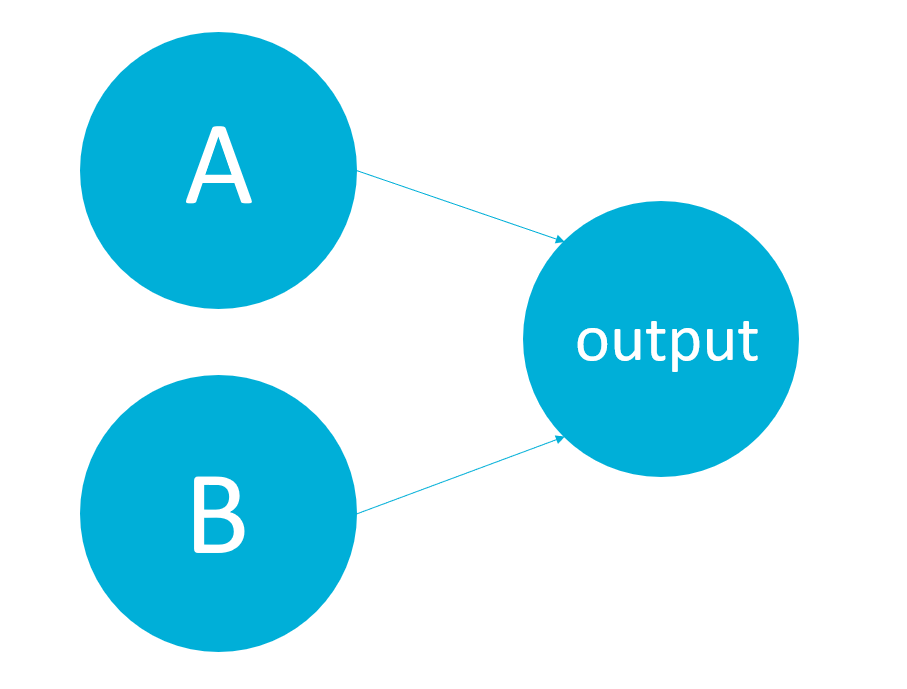
Veel simpeler dan dat worden neurale netwerken niet. Google maar eens op afbeeldingen van neurale netwerken, ze hebben allemaal veel meer neuronen en meer lagen, maar die ga ik niet allemaal in Excel programmeren en we hebben er ook niet meer nodig (eigenlijk wel, maar dat komt pas later.)
In het neurale netwerk krijgen A en B de waardes waar of onwaar. Dat representeren we als 1 voor waar en 0 voor onwaar (dat rekent een stuk makkelijker dan tekst). De verbindingen van A en B naar de output neuron hebben een gewicht. Dat zorgt er voor dat A en B niet even zwaar hoeven mee te wegen voor de beslissing. Als de verbinding van A een gewicht heeft van 0.2 en die van B 0.7 dan betekent dat als A waar is (dus 1) de output neuron de waarde heeft van 0.2. Als B aanstaat 0.7, en als ze allebei aanstaan 0.9.
Een waarde van 0.2 zegt in ons geval niet zoveel, iets kon waar zijn (1) of onwaar (0), wat 0.2 is weten we niet, daarom krijgt de output neuron een zogenaamde ‘actiepotentiaal grenswaarde’. Dat is de waarde die in ons supersimpele neuron uitleg bepaalt of het signaal doorgestuurd moet worden of niet. Komt de waarde van het signaal dat binnen komt boven deze waarde dan is de uitkomst 1 anders is deze 0. Stel we zetten de grenswaarde in ons voorbeeld op 0.6 dan gaat deze af zodra B waar is en maakt het eigenlijk niet uit of A wel of niet waar is. Hetgeen je zou kunnen schrijven met operatoren als: (A of niet A) en B. Of simpeler als: B. Willen we de ‘en’ operator simuleren dan moet de grenswaarde hoger liggen bijvoorbeeld op 0.8 want dan zijn opgeteld A en B genoeg om boven die waarde te komen. Voor ‘of’ moet hij een stuk lager liggen, bijvoorbeeld 0.1.
Maar hoe kan het netwerk deze waardes nou zelf leren? Daarvoor gebruiken we een versimpelde versie van een strategie met de naam backpropagation. Het idee is dat je het netwerk in het begin willekeurige waardes geeft voor de gewichten en grenswaarde(s) en dan vervolgens de uitkomsten dat het geeft gaat beoordelen, is het goed? Prima, niets aan doen, is het fout, dan moeten de waardes aangepast worden. Je begint hierbij aan het einde van het netwerk en werkt je weg terug. Dat is voor ons gelukkig een hele korte reis.
Als de uitkomst van het netwerk niet overeenkomt met het goede antwoord, dan passen we de actiepotentiaalgrenswaarde aan, dacht het netwerk 1 en was het 0, gaat de waarde omhoog, want we willen voorkomen dat hij bij de binnengekomen waarde afgaat en daarvoor moet je zorgen dat de grenswaarde boven de input waarde ligt, dat doet hij nu duidelijk nog niet. Omgekeerd als het netwerk 0 gokt en het had 1 moeten zijn gaat de grenswaarde naar beneden. Voor de wegingen van A en B naar de output neuron passen we de waarde willekeurig naar boven of beneden aan. Dat is niet de mooiste oplossing, maar ik wil niet te veel intelligentie in de foutcode stoppen voor een dergelijk simpel netwerk, dat voelt als valsspelen.
De Excel staat hier ik heb de functies EN, OF en NEN gemaakt, als je wilt kan je zelf NOF er ook nog inbouwen. Het gaat afhankelijk van de startwaardes en een beetje mazzel goed voor deze 3 operatoren. Ik laat het als huiswerkopdracht (ik ben al weer ruim over de 1000 woorden heen) waarom dit netwerk te klein is voor de EXOF. Kom je daar echt niet uit moet je maar een mailtje sturen of aanschieten op LinkedIn.
Leren ExcelerenMijn ouders zitten terwijl ik dit blog schrijf in Moldavië. Mijn moeder had in het hotel waar ze overnachtte problemen met de Wifi-verbinding van haar telefoon. Een ter hulp geroepen hotelbediende lukte het vervolgens wel de koppeling tot stand te brengen. Deze dame sprak na het oplossen van het probleem de woorden: ‘It’s magic’. Toen ik dat verhaal hoorde, was mijn eerste reactie: “Hé, dat is mijn tekst! Ik zal die lui in Moldavië eens laten zien wie hier de software magiër is”. Ik had toen eigenlijk het huidige blog al opgegeven, maar dat weerhield me niet om er nog eens met een frisse blik tegen aan te kijken.
De missie: schrijf een AI in ’s werelds meest gebruikte en meest veelzijdig ingezette bedrijfsapplicatie: Microsoft Excel. Nou is dat niet zo heel erg ingewikkeld. Excel heeft namelijk een volwaardige programmeertaal ingebakken in de ontwikkelaarsmodus. Maar dat is niet echt een uitdaging, daarom was het idee om voor de AI uitsluitend ingebakken Excelformules te gebruiken.
In theorie moet dat kunnen. Excel heeft genoeg veelzijdige formules die zou je kunnen gebruiken als functies en dan heb je een, zij het hele rudimentaire, functionele programmeertaal. In de praktijk echter is het absoluut gekkenwerk en ik heb ook nog andere hobby’s. Bovendien: wat heb ik hotelmedewerkers in Moldavië te bewijzen? Dus na een goede 18 minuten heb ik besloten dat het geheel heel erg te versimpelen. Wat is het allerminste wat ik nog kan kwalificeren als een kunstmatige intelligentie? Dat is altijd een discutabele vraag, maar ik heb het gevoel dat ik met een kennissysteem nog wel weg kan komen. Een kennissysteem is een computersysteem dat menselijke kennis bevat en dat gebruikt om een probleem op te lossen. Als dat klinkt als elk computersysteem, tja dat doet het ook, maar zoals ik zei, ik ben aan het versimpelen. Als je daar problemen mee hebt stel ik voor dat je eerst een paar uur een neuraal netwerk in Excel formules probeert te bouwen, vervolgens op Wikipedia de pagina over expertsystemen leest, deze podcast luistert waarin iemand van Microsoft zegt dat een rekenmachine al KI is en dan net als ik je schouders ophaalt en pakt wat je pakken kan.
Dus een expertsysteem. Een goed voorbeeld van een expertsysteem is een diagnosesysteem. Je geeft je symptomen op, het systeem stelt aan de hand daarvan een aantal vragen en trekt vervolgens op basis van jouw symptomen en jouw antwoorden een conclusie. Een ander bekend voorbeeld zijn die 20-questions-spelletjes die met 20 ja/nee-vragen raden welk bekend persoon je in je hoofd hebt. Dat is nog steeds best wel ingewikkeld en ik was enorm aan het versimpelen (ik neem het versimpelen op dit moment erg serieus!) dus we gaan op het randje zitten van wat je nog een expertsysteem mag noemen. Een heel bekend voorbeeld (zeker voor ouders) van een expertsysteem is de Apgartest. Voor elke baby checkt een arts 5 kritieke onderdelen. Op elk onderdeel kun je 0,1 of 2 punten scoren. Deze punten tel je op en voor het resultaat geldt de vuistregel dat als je een ruime voldoende scoort er (waarschijnlijk) niets aan de hand is. Scoor je een onvoldoende dan staat er binnen no-time een heel doktersteam in de kamer.
Vandaag houden we het expertsysteem iets luchtiger en gaan we een eenvoudig boekhoudprogramma in elkaar zetten. Daarvoor richten we een fictieve klaverjasbedrijfscompetitie op binnen Orcado. (Die competitie is fictief, want ondanks dat meerdere van mijn collega’s kunnen klaverjassen hebben ze het nog nooit aangedurfd om daadwerkelijk tegen me te klaverjassen. Dat neem ik ze overig niet kwalijk, van de 4 kampioenschappen die ik vorig jaar heb gewonnen, was maar één een badmintonkampioenschap, de rest waren klaverjasoverwinningen.) Het belangrijkste van een fictieve competitie is natuurlijk de naam. Na een bijzonder korte brainstormsessie is dat geworden: Harten ITwee. De competitie heeft natuurlijk een financiële afrekening (waarom anders een boekhoudprogramma?). Een goede financiële afrekening voldoet aan een aantal regels (regels die een expert kent).
1. Er is een baten- en een lastenpost.
2. De baten en lasten moeten onder streep gelijk zijn.
3. Je moet van alle baten en lasten een bewijs/afschrift hebben.
4. Het verschil tussen je baten en lasten is een overschot/tekort, dat wordt verrekend met je kas
Die regels zetten we in ons Exceldocument, dat je hier kunt vinden. Vervolgens gaan we aan de hand van Excelformules controleren of aan die regels wordt voldaan. Maar voor dat het zover is gaan we eerst een nieuwe naam bedenken want Harten ITwee is toch het resultaat van een duidelijk té korte brainstormsessie, aan de andere kant is het ook weer niet zó belangrijk, we noemen het wel… uhm… Seinen op eigen wijze.
De eerste regel is simpel, we moeten minstens 1 baat en 1 last hebben, dus als E2, F2, G2 en H2 alle 4 niet leeg zijn hebben we daar aan voldaan. De formule wordt iets ingewikkelder omdat we ook willen laten zien welke er mist, maar het hoeft ook niet te ingewikkeld. Als er 2 missen vind ik het genoeg dat hij de eerste laat zien, en zodra je dat fixt de ander. In Excelformules kan dat zo:
=ALS(ISLEEG(E2);"Er is geen baat met een omschrijving" ;ALS(ISLEEG(F2);"Er is geen baat met een waarde" ;ALS(ISLEEG(G2);"Er is geen last met een omschrijving" ;ALS(ISLEEG(H2);"Er is geen last met een waarde" ;""))))
Het ziet er niet heel elegant uit maar het werkt. Het zijn eigenlijk gewoon geneste if-statements: Als E2 leeg is geef de tekst dat er geen baat is met een omschrijving anders, als F2 leeg is, et cetera. Ter vergelijking als je dit herschrijft naar javascript en dezelfde logica gebruikt ziet dat er zo uit:
if(E2 === ""){ return "Er is geen baat met een omschrijving" } else if (F2 === "") { return "Er is geen baat met een waarde" } else if (G2 === "") { return "Er is geen last met een omschrijving" } else if (H2 === "") { return "Er is geen last met een waarde" } else{ return "" }
, wat je zou kunnen herschrijven als:
if (E2 === "") { return "Er is geen baat met een omschrijving" } if (F2 === "") { return "Er is geen baat met een waarde" } if (G2 === "") { return "Er is geen last met een omschrijving" } if (H2 === "") { return "Er is geen last met een waarde" } return ""
Dat is al een heel stuk leesbaarder, maar dat is niet in Excel en we moeten troeven met de kaarten die we hebben, dus op naar de volgende regels.
De volgende regel is ook erg makkelijk. We sommeren de baten en de lasten en kijken of die dan ongelijk zijn:
=ALS(J2<>K2;"Baten en lasten zijn ongelijk";"")
Regel 3 is een grotere boef. Om dat makkelijk op te lossen, maken we wat extra hulpvelden. In kolom P komt een opsomming van alle bedragen die ontvangen en uitgegeven zijn. Dit is de uitgebreide versie van kolom E en G. Je kunt er ook voor kiezen om daar alles uit te schrijven en de kwitanties van baten en lasten te scheiden, maar dat heb ik hier niet gedaan. Vervolgens maken we een nieuw blad en zetten we in kolom A de omschrijving en daarnaast een foto van de kwitantie. Daarna vullen we kolom Q met de volgende formule:
=ALS.FOUT(HYPERLINK("#'bijlages'!" & ADRES(VERGELIJKEN($P2; bijlages!$A:$A; 0); 1); TEKST.SAMENVOEGEN("afb "; $P2));"")
We maken hier een hyperlink naar het bijlageblad, zoeken dan op dat blad in kolom A de waarde van P2 (dit is Q2, in Q5 staat daar P5) en dan linken we naar de cel waar die waarde in staat. We geven die link het naampje afb + P2. Daarom heen staat een ‘als.fout’, voor als er niks gevonden kan worden. In dat geval laten we het veld leeg. Wacht. Ik zal het opsplitsen. Dat maakt het wat leesbaarder:
=ALS.FOUT( // ALS.FOUT(waarde;waarde_indien_fout) HYPERLINK( // HYPERLINK (koppelingslocatie; [vriendelijke_naam]) "#'bijlages'!" & ADRES( // ADRES(rij_getal; kolom_getal;[abs_getal];[a1];[blad_tekst]) VERGELIJKEN( // VERGELIJKEN(zoekwaarde; zoeken_matrix;[criteriumtype_getal]) $P2; bijlages!$A: $A; 0); 1); TEKST.SAMENVOEGEN( // TEKST.SAMENVOEGEN(tekst1;[tekst2];...) "afb "; $P2) ); "")
Is dat leesbaarder? Ben je ook niet blij dat ik het simpel heb gehouden? De manier waarop je in Excel formules nest maakt het lastig om te lezen wat er precies gebeurt. Gelukkig is de volgende formule een stuk makkelijk te volgen in kolom R:
=ALS(EN((P2<>"");Q2="");1;0)
Daar staat zoveel als: als P2 niet leeg is EN Q2 is wel leeg, dan 1 anders 0. Vervolgens sommeren we over kolom R en dat geeft ons het aantal missende bijlages. Dat zetten we dan bij de derde regel met:
=ALS(J5>0;""& J5 &" missende bijlage(s)";"")
Als het totaal van missende bijlages groter is dan 0, geef dat aantal en plak daar ‘ missende bijlage(s)’ aan vast. In ons voorbeeld is dat zo in 1 geval. Ik heb nog geen contributie overgemaakt. (Maar gezien ik deze fictieve klaverjascompetitie sowieso ga winnen verrekenen we dat later wel met het prijzengeld.)
Je ziet overigens dat ik twee manieren van tekst aan elkaar plakken door elkaar gebruik:
"aan" & "elkaar" //en TEKST.SAMENVOEGEN("aan","elkaar")
In dat opzicht zijn Excelformules net een echte programmeertaal: meer oplossingen voor hetzelfde probleem.
Dan moeten we nog de laatste regel: Het verschil tussen je baten en lasten is een overschot/tekort, dat wordt verrekend met je kas. Dat laat ik voor jullie als huiswerkopdracht want ik zit al weer over de 1500 woorden. Je hebt hiervoor de adres- en vergelijkenfuncties nodig van regel 2 of je kunt verticaal zoeken gebruiken. Ik ga me niet in die discussie mengen. Zodra je dat huiswerk hebt gedaan heb je een volledig werkende kunstmatige intelligentie in Excel. Voelt het alsof we echt een kunstmatige intelligentie in Excel hebben gemaakt? Nee, maar was het al het geklooi met Excel uiteindelijk waard? Ook nee, maar zijn we uiteindelijk op zijn minst tevreden over de naam van onze fictieve klaverjas vereniging? Ook nee, dáár kunnen we gelukkig nog iets aan doen. Ehm wat vinden jullie van klaverJSen, of KlaverClass, of 3-kaarten logica, of Klaverjasegmentation fault, of KlaverjAS2en, of, of, of…
Disclaimer: Omdat deze exercitie (ook voor mij) niet AI genoeg aanvoelde volgt binnenkort(ish) het blog Leren Exceleren 2, waarin in ik alsnog een neuraal netwerk bouw in Excel, dat 2-waarde logica statements kan leren.
De psychologie van een paarse banaan en gevaarlijke algoritmesMeestal knal ik de blogs er in een paar uur uit, gaan die door naar de editor, volgt er een stukje spellingscontrole waar Word nog heel wat van kan leren, en dan verschijnt de blog online. Dit blog is anders, dit blog is al in revisie sinds februari, een blog over driewaardenlogica had allang online kunnen staan, maar ik wilde het over discriminatie hebben, en dat is een stukje lastiger. Tja, verschil moet er zijn.
Discriminatie betekent letterlijk onderscheid maken en daar is niets mis mee. Het splitsen van even en oneven getallen is bijvoorbeeld discriminatie, maar daar zal vrijwel niemand iets tegen hebben. Ik ga het echter hebben over een speciaal geval van discriminatie: racisme. Hoe je het wendt of keert, racisme is slecht, daar zijn we het wel over eens, toch? Helaas bestaat het wel en met de komst van kunstmatige intelligentie is het risico van onbedoeld racistische software een serieus gevaar. (Bedoeld racistische software is al sinds het begin van software een gevaar, laten we de KKK niet leren programmeren.)
Maar met zelflerende algoritmes gaat het onbedoeld ook fout en daar wordt dan ook voor gewaarschuwd door bijvoorbeeld de New York Times, of recenter de NOS. Ja, dat laatste bericht is uit mei. Dat is het nadeel als je lang over je blog doet, dan word je ingehaald door de NOS. Er worden in beide artikelen redenen gegeven voor waarom de algoritmes racistisch zijn geworden, maar het probleem ligt volgens mij dieper. Het ultieme doel van kunstmatige intelligentie is het nabootsen van menselijke intelligentie. Er zijn (helaas schrikbarend veel) racistische mensen, dus als je dat nabootst krijg je racistische machines. De vraag is dus, waarom zijn mensen racistisch?
Er zijn twee richtingen in de psychologie die het proberen te verklaren (er zijn er nog wel meer, maar ik zit al aan de 300 woorden, en ik ben er nog lang niet…) groepsgedrag en prototypering. Laten we beginnen met groepsgedrag, het idee is dat er een dierlijk instinct is dat je in een groep veiliger bent voor roofdieren (niet dat we ons in het dagelijks leven nog echt zorgen hoeven te maken over roofdieren, maar die instincten zitten heel diep). Het idee is dat je een groep maakt met iedereen die zoveel mogelijk op je lijkt en dan is het vervolgens met zijn allen tegen de rest. Over dit fenomeen is een aantal bekende films gemaakt zoals The Wave en Das Experiment. Mocht je die nog niet hebben gezien, ik vind ze aanraders. De film is gebaseerd op het Stanford prison experiment. Op dat onderzoek is veel kritiek, we moeten dus een beetje oppassen om het als pure waarheid aan te nemen, maar het is niet het enige onderzoek. In het experiment wordt veel gesproken over groepsdruk. Dat mensen onder druk heel ver kunnen gaan wordt ook bewezen door Milgram die in zijn onderzoeken schokkende resultaten laat zien. Nou is er ook veel kritiek over die experimenten, maar die gaan hoofdzakelijk over de ethiek er van.
Een ander bekend onderzoek toegespitst op discriminatie is dat van Jane Elliott waarin ze basisschool kinderen onderverdeelt op basis van hun oogkleur. Het laat zien dat de kinderen die op basis van hun oogkleur in de superieure groep zijn geplaatst zich ook superieur gaan gedragen. Als de rollen omgedraaid worden gebeurt hetzelfde, alhoewel wel in afgezwakte mate. Hoewel het de opzet van dit experiment was om discriminatie te laten zien en daardoor af te zwakken, geeft het goed weer hoe snel mensen opsplitsing in groepen accepteren en zich er naar gaan gedragen.
Hoewel dat een aardig verklaring lijkt, iedereen behoort tot zijn eigen groep en iedereen die buiten die groep valt wordt met een schuin oog aangekeken, blijft er toch nog wel iets knagen. Er is namelijk een probleem. In de hier genoemde onderzoeken worden mensen arbitrair in de groepen verdeeld. Het verklaart niet hoe er een overkoepelende groep is van mensen die je nog nooit eerder hebt gezien, terwijl onderzoek laat zien dat ook daar discriminatie duidelijk aanwezig is. Er is zelfs uit onderzoek gebleken dat kinderen een positievere blik hebben op witte dieren dan op zwarte dieren. Een verklaring daarvoor? Prototypering. Na een hele reeks zorgelijke menselijke eigenschappen tijd voor een klein stukje goed nieuws, want in prototypering zijn we als mensen dan weer heel goed. We gebruiken het bij iets anders waar we heel goed in zijn, object herkenning. Om dat uit te leggen wil ik je vragen om voor jezelf een banaan te omschrijven. Dan ga ik in de volgende alinea kijken of die van mij daar een beetje mee overeenkomt.
Geel en krom fruit. Was het een beetje in de richting? De banaan is een stuk fruit, dat staat buiten kijf (hoewel wat fruit is nog wel een discussie kan zijn), maar dat hij geel en krom is, dat is niet persé altijd waar. De banaan is krom door de zwaartekracht, door de plant geforceerd schuin te houden kan je een perfect rechte banaan kweken. Bovendien begint een banaan groen en eindigt hij bruin, maar zelfs als we hem paars verven, is het dan geen banaan meer? Dus hoewel geel en krom belangrijke karakteristieken zijn om de banaan van ander fruit te onderscheiden zouden we nog steeds wel een banaan herkennen als hij paars en recht was. Het gaat echter niet zo snel als het herkennen van een prototypische banaan en daar zit hem de crux. Er is een prototype van een betrouwbaar persoon in de westerse samenleving en ook een prototypisch onbetrouwbaar persoon.
Beeld je maar eens een gangmember in en daarnaast een gangster. Grote kans dat de gangmember grote gouden kettingen heeft, een afgezakte broek en zijn pistool super ineffectief schuin houdt, terwijl de gangster in een Armani-pak loopt. Die kans is groter omdat je ze tegelijkertijd moest inbeelden en dus onderscheid moest maken tussen de twee. Deze manier van objectherkenning is dus eigenlijk van nature discriminatoir, het is namelijk super effectief om in hokjes te denken. Een auto heeft 4 wielen en een fiets 2. Het is absoluut niet altijd waar, maar vaak genoeg om er gebruik van te kunnen maken. Laat dat nou ook de manier zijn waarop we computers objecten laten herkennen.
Onze hersenen zijn één groot netwerk van neuronen die met kleine elektrische signalen samen dingen beslissen. Om computers ook goed te maken in objectherkenning wordt er gebruik gemaakt van artificiële neurale netwerken. Dat werkt bijzonder goed. Zo kan Googles Vision algoritme al zonder probleem omgaan met een paarse banaan:
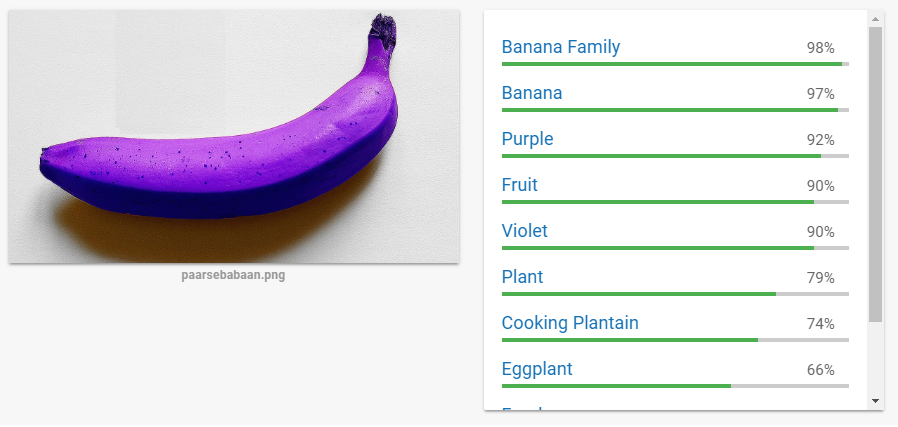
Als we het iets ingewikkelder maken door een rechte banaan te nemen en een beetje lelijk de randjes weg te fotoshoppen krijgen we het algoritme nog wel in de war:

Ik kan me echter voorstellen dat je daar zelf ook even een tweede keer naar moest kijken.
Maar als we de computers maken zoals wij zijn, en wij zijn racistisch, maken we dan niet ook automatisch racistische computers? Het zou mooi zijn als de computers “beter” worden dan wij, maar kan je iets maken dat op alle mogelijke vlakken slimmer is dan jezelf bent? Artificiële intelligentie blijft een lastig iets.
Leren programmeren (duel)leren (deel 4)Jullie hebben nog een uitslag van me te goed. Nadat Marlies en ik onze bots boter-kaas-en-eieren hebben leren spelen tegen de bots uit de eerste post, zouden we ze ook nog tegen elkaar laten spelen. Voor dat ik jullie vertel wat de uitslag is, eerst even de spelregels:
Dan de voorspellingen. Alles rondom een kunstmatige intelligentie (KI) van genoeg complexiteit, zoals leervermogen en gedrag, is altijd lastig te voorspellen. Dat is één van de nadelen van het gebruik van KI in kritische systemen. Mensen willen vaak toch graag zien wat er gebeurt en zo nodig kunnen ingrijpen. Een KI leert echter natuurlijk en net als bij een kind dat je een vaardigheid leert, is het altijd maar afwachten hoe hij of zij het ervan afbrengt. Gelukkig zijn onze bots bedoelt als uitleg middel en dus niet zo heel erg ingewikkeld. Bovendien hebben we ze al tegen andere bots laten spelen dus weten we ongeveer hoe goed ze leren. Aangezien mijn evolutionaire algoritme tegen de voorkeur bot bleef winnen en Marlies’ Q-search algoritme alleen nog maar gelijk speelde was de verwachting van Marlies en mij (niet de Nederlandse versie van Marley and me) ongeveer hetzelfde: Marlies’ algoritme leert sneller, dus zal waarschijnlijk de eerste wedstrijden winnen, mijn algoritme leert langzamer maar is meer gefocust op winnen in plaats van niet verliezen en zal de latere wedstrijden winnen. Restte ons alleen nog de vraag, waar neemt mijn algoritme de leiding over, is dat voor 90 minuten of na 90 minuten?
(Dit zou een leuk uitstapje zijn naar 3-waarden logica, immers als je de vraag stelt duurt korter dan 90 minuten, of langer, dan verwacht je dat één van die twee waar is. Dat is echter niet het geval. Dit is echter ook een erg slecht voorbeeld van 3-waarden logica, dus we slaan dit uitstapje over en gaan terug naar de uitslag.)
Nooit, het antwoord is nooit. Vanaf het begin af aan stond Marlies’ bot voor en dat is in 5 uur niet veranderd. Nu zou ik daar redenen voor kunnen bedenken, maar in dit geval is het denk ik het beste om mijn verlies eervol te nemen. Marlies gefeliciteerd!
Eindstand na 5 uur:
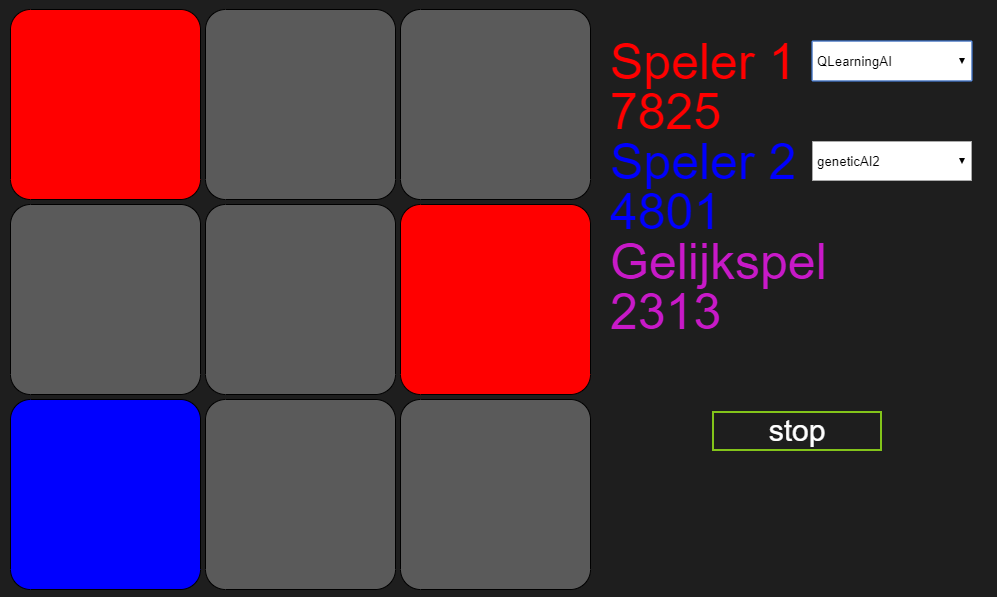
Het leuke van een KI is dat voor het algoritme de regels er niet toe doen. Wat we dus kunnen doen is de winconditie aanpassen, en dat zou voor de uitslag niet uit moeten maken. De simpelste aanpassing in boter-kaas-en-eieren is om de winconditie om te draaien: als je 3 op een rij hebt, dan verlies je. Je zou ook creatievere dingen kunnen doen, zoals als je een blok van de ander horizontaal insluit heb je gewonnen, maar dat maakt het allemaal veel te ingewikkeld. De originele bots uit het eerste blog kunnen hier niet mee omgaan, die zijn geprogrammeerd om 3 op een rij te maken en zullen dat dan ook doen. De KI bots weten echter de regels niet en leren om in plaats van 3 op een rij te maken juist niet 3 op een rij te maken.
Met de winconditie omgedraaid wordt het spelletje wezenlijk anders. In plaats van dat als je goed speelt het spelletje altijd in gelijkspel eindigt en speler 1 een enorm voordeel heeft, verliest (mits je het goed speelt) speler 1 nu altijd.
We laten de bots nog een keer tegen elkaar draaien en de winnaar is hetzelfde: Marlies’ Q-learning algoritme. Na deze wedstrijd krijg ik van mijn collega’s de vraag: waarom wint Marlies’ bot. Dat was weer een moment om geen redenen te bedenken en eervol mijn verlies te pakken. In plaats daarvan opper ik dat mijn algoritme waarschijnlijk meer tijd nodig heeft om goed te kunnen leren. Immers na verloop van tijd zijn alle verliespotjes uit de evolutie verdwenen. Om die theorie te testen laten we de bots wat langer tegen elkaar spelen.
Na 3 dagen:
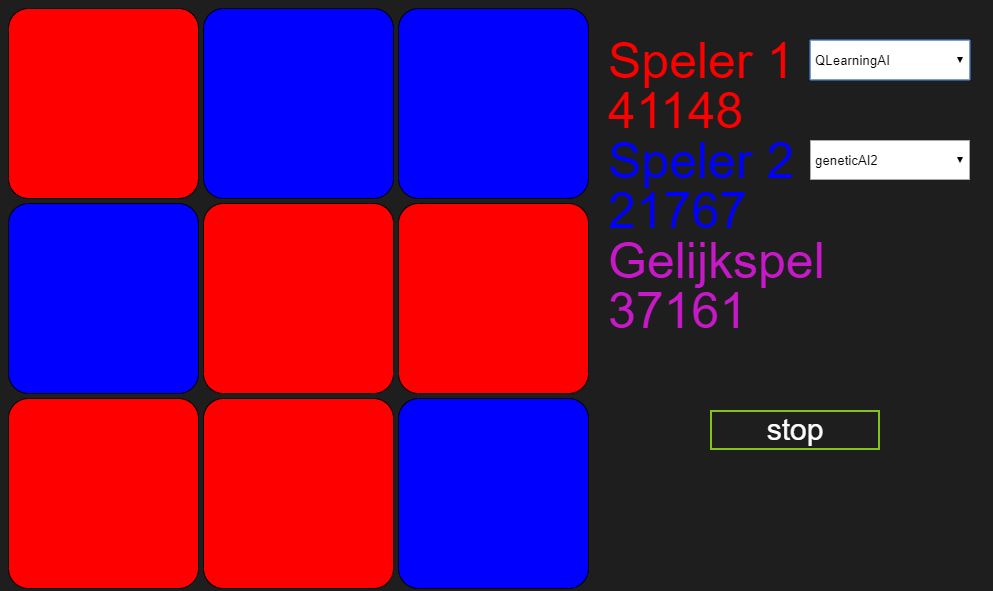
Na 6 dagen:
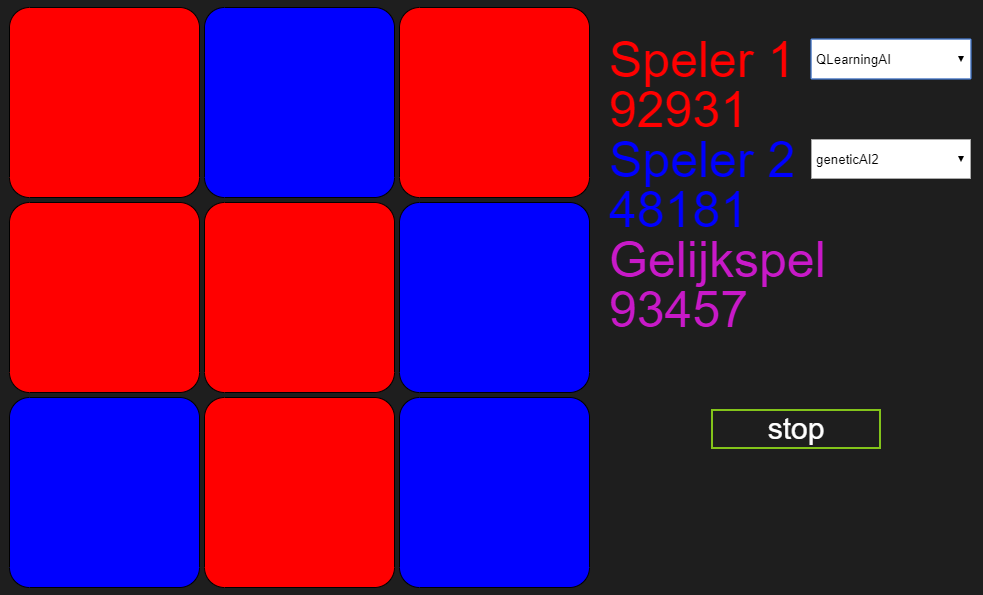
Na 9 dagen:
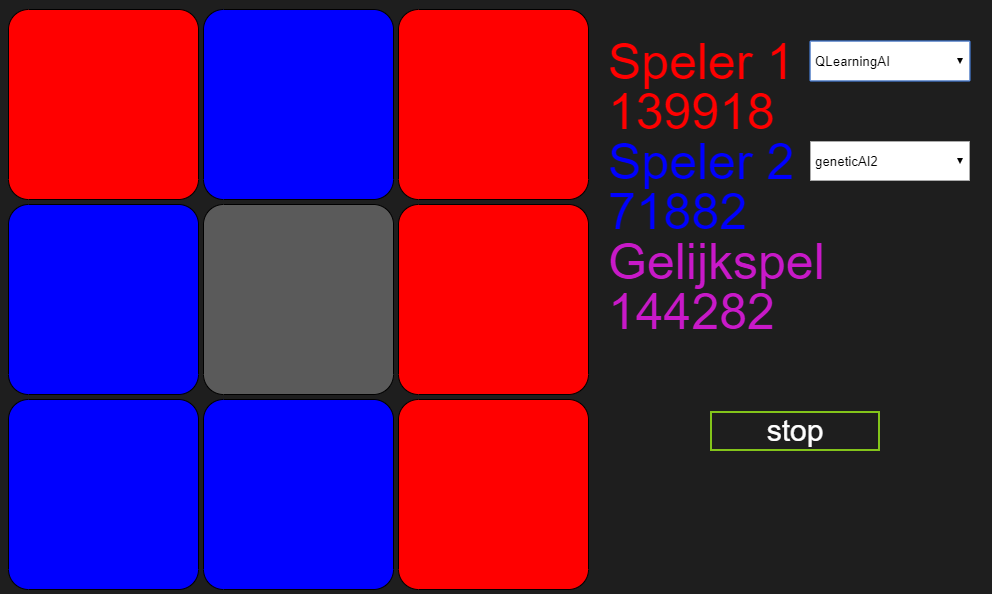
Na 24 dagen:
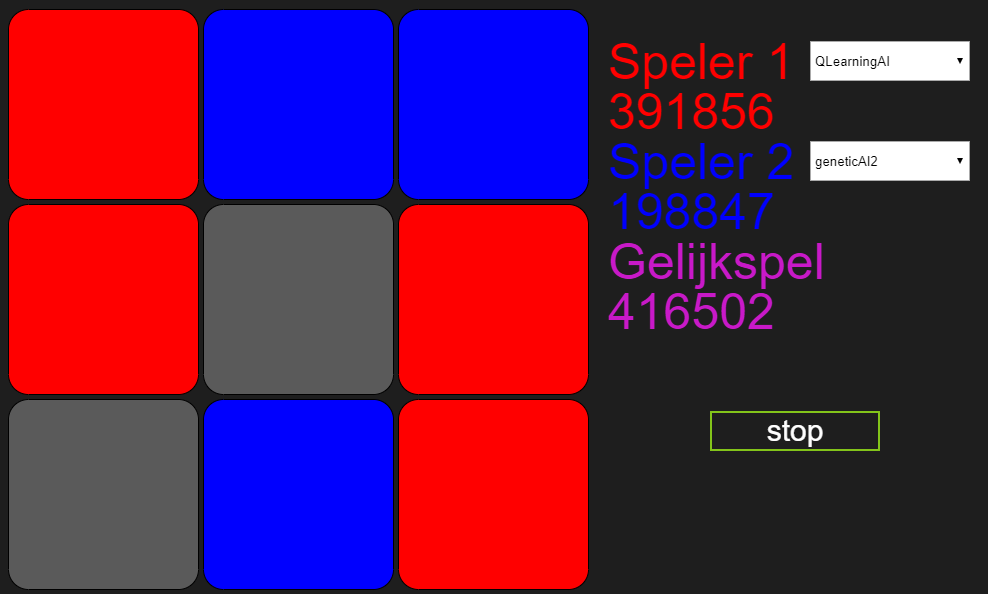
Na 30 dagen:
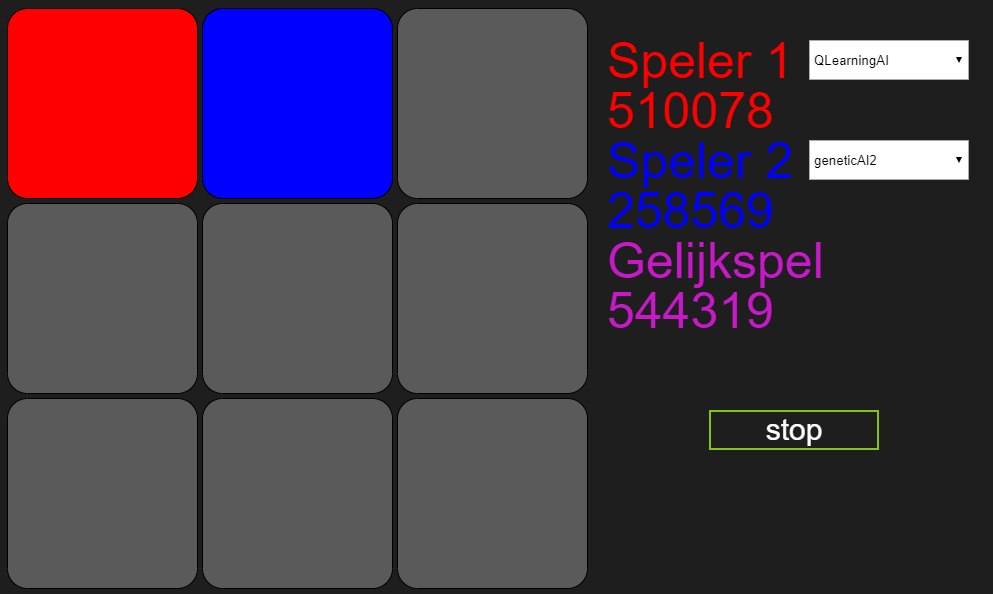
Na een maand de bots te laten strijden en ruim een miljoen spelletjes later, blijkt maar weer dat ik net zo goed direct eervol mijn verlies had kunnen pakken. Had ik die laptop bitcoin kunnen laten minen, had ik er nog iets aan gehad. Ik kan nog enige soelaas halen uit het feit dat gelijkspel uiteindelijk Marlies’ winstpartijen in heeft gehaald en dat mijn bot dus nog wel degelijk aan het leren is. Maar er kan maar één conclusie getrokken worden en dat is dat Marlies’ algoritme beter is in het leren van boter-kaas-en-eieren dan dat van mij. Dus ook hier nog maar een keer: Marlies, gefeliciteerd!
Leren programmeren (duel)leren (deel 3)Gelukkig heeft Daan in zijn vorige blog al gezegd dat ik niet ook zo’n heel verhaal aan elkaar hoef te ratelen, pfew. Het enige waar ik voor moet zorgen is dat je na afloop het woordgrapje uit de vorige blog begrijpt. En dat er tussendoor nog iets over een lerend algoritme is uitgelegd.
Om boter-kaas-en-eieren te leren maak ik gebruik van een algoritme dat heel kort door de bocht als volgt kan worden uitgelegd. Stel dat je geen idee hebt hoe boter-kaas-en-eieren werkt. In plaats van het je vriendelijk uit te leggen, gaan we gewoon spelen. Wel vertel ik je dat je alleen maar kruisjes mag zetten, op plekken waar nog geen kruisjes of rondjes staan. Na een tijdje laat ik je weten dat het spel is afgelopen en dat je hebt verloren. In theorie kan je natuurlijk ook hebben gelijk gespeeld of zelfs hebben gewonnen, maar hé, je kende de regels nog niet en ik wel, dus daar ga ik niet vanuit. Vervolgens spelen we het nog een keer. En dat nog heel erg vaak. In de loop van tijd krijg je door hoe je kan voorkomen dat je verliest, of misschien zelfs hoe je kan winnen.
Nu is het waarschijnlijk dat jij door zou krijgen dat er een relatie is tussen 3 rondjes of kruisjes op een rij, en winst of gelijkspel of verlies. Dat is niet hoe mijn AI het doet. Mijn AI maakt gebruikt van een algoritme met de naam Q-learning, en is een variant van reinforcement learning. Je zou nu het woordgrapje moeten snappen, dan kan ik me richten op het uitleggen van het lerende algoritme. Het idee achter reinforcement learning is dat je leert door middel van de feedback die wordt geleverd, in dit geval dus of je hebt verloren, gelijk gespeeld, of gewonnen. Deze bot kan je hier uitproberen – http://undercover.horse/tictacque/ !
Reinforcement learning is gebaseerd op het behaviourism, dit is een stroming in de psychologie over gedrag. Hierin wordt gekeken hoe gedrag ontstaat onder invloed van de omgeving. Dit is een goed voorbeeld van hoe ideeën uit de psychologie worden gebruikt bij kunstmatige intelligentie. Reinforcement learning doet het meest denken aan (operante) conditionering. Hierin wordt in een bepaalde context op een bepaald gedrag altijd een beloning of straf gegeven, op die manier leert een dier of mens wat wenselijk gedrag is.
Het voordeel van Q-learning is dat je van tevoren niet hoeft te weten welke situaties kunnen voorkomen, en dus ook de bijbehorende mogelijke acties niet kent. Om te leren, wordt er een lijst bijgehouden met alle situaties die zijn tegengekomen inclusief welke zet hierin is gedaan, en een getal dat aangeeft hoe goed de uitkomst was. Die laatste is de q-waarde. Met deze lijst kan je later in dezelfde situatie dus zetten vergelijken, en degene met de hoogste q-waarde kiezen. Maar aan het begin van het spel is deze lijst helemaal leeg. Je moet dus q-waarden gaan leren.
De q-waarde wordt na iedere beurt geüpdatet, op basis van wat de q-waarde op dat moment is, en de nieuwe informatie. Deze nieuwe informatie bestaat uit de feedback, dus hoe goed de zet was, en wat de toekomstige mogelijkheden zijn. Bij boter-kaas-en-eieren is het eerste moment van feedback officieel pas als het spel is afgelopen. Hier is winst +1 punt, verlies -1, en gelijkspel 0. Daarnaast geef ik ook 0 punten aan een spel dat nog niet is afgelopen. Hoe goed de toekomstige mogelijkheden zijn, wordt bepaald door de hoogste q-waarde van de situatie waar je in bent beland. Als je het spel dus voor de eerste keer speelt, weet je pas iets als het is afgelopen. De waardes bij alles tot het einde blijven dan 0, terwijl de laatste situatie + actie wordt geüpdatet aan de hand van de feedback. Op die manier leer je steeds een stukje verder terug wat wel en geen goede zetten zijn.
Een van de gevaren hiervan is dat je een suboptimale strategie leert. Daarom is het belangrijk om te onderzoeken of er nog meer mogelijkheden zijn. Eén van de andere gevaren, is dat je altijd blijft rondkijken voor betere mogelijkheden. In dat geval weet je wel hoe je het spel perfect moet spelen, maar maak je nooit gebruik van deze kennis. Om dit te voorkomen wordt een andere lijst bijgehouden, met hoe vaak een combinatie van situatie en actie zijn voorgekomen. Als je in een situatie komt, waarin je de volgende zet moet kiezen, wordt er voor alle mogelijke zetten die minder dan 3 keer zijn gedaan niet uitgegaan van een q-waarde, maar van een gezonde nieuwsgierigheid. Op het moment dat dan de q-waarde wordt opgevraagd, wordt een optimistische waarde teruggegeven, in plaats van wat de q-waarde op dat moment is (als die dan al bestaat).
Wat je bij voorkeurAI1 ziet, is dat mijn algoritme, die ik QlearningAI heb genoemd, aan het begin van het spel alles een keer probeert, maar na een tijdje constant dezelfde tactiek uitvoert. Dat ziet er als volgt uit:
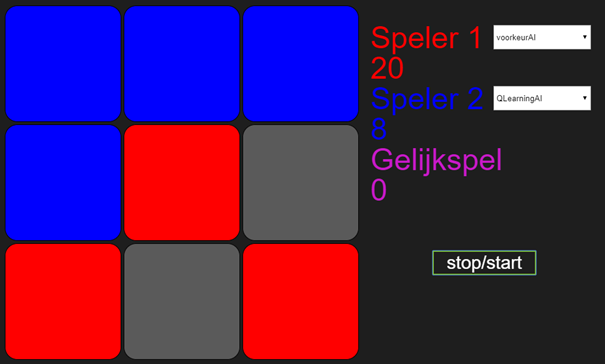
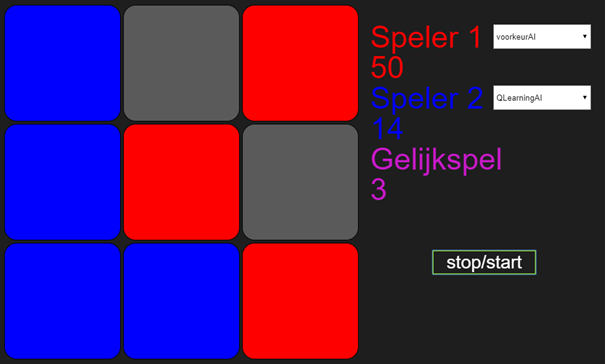
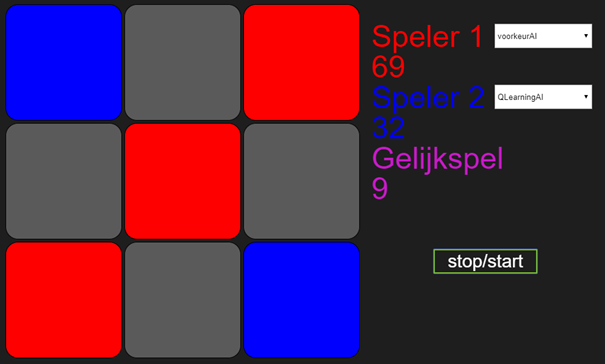
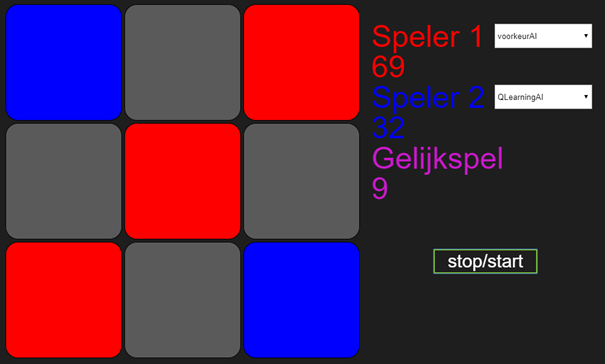
Wat je ziet is dat de VoorkeurAI1 aan het begin nog de meeste spelletjes wint, maar vanaf 69 gewonnen spellen, wint QLearningAI alles.
Tegen VoorkeurAI2 gebeurt bijna hetzelfde, behalve dat VoorkeurAI2 een tactiek heeft om verlies tegen te gaan. De QLearningAgent wint daarom niet alles, maar het wordt constant gelijk spel, zoals getoond in de volgende plaatjes.
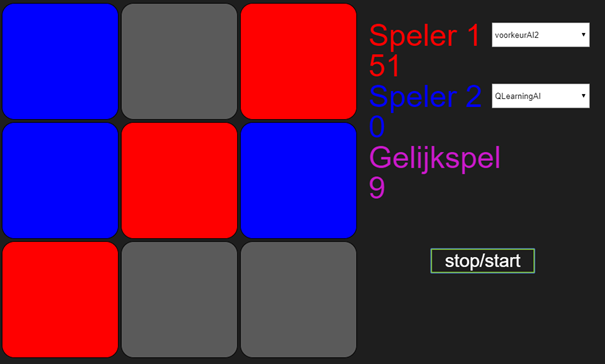

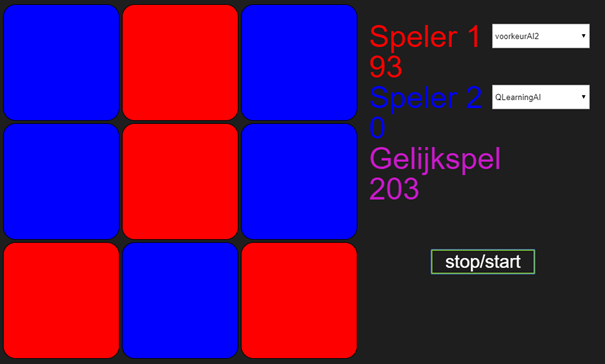
Mij vallen hier drie dingen in op. Ten eerste dat QLearningAI er tegen VoorkeurAI2 langer over doet om nooit meer te verliezen in vergelijking met VoorkeurAI1. Ik denk dat dit komt door het verschil in feedback tussen winst en gelijkspel, waardoor er sneller wordt geleerd als er wordt gewonnen. Ten tweede valt me op dat QLearningAI veel sneller dan GeneticAI2 van Daan leert tegen VoorkeurAI2. Als laatste, daarentegen, lukt het GeneticAI2 uiteindelijk wel om te winnen van VoorkeurAI2, terwijl QlearningAI blijft hangen in gelijkspel. Hopelijk is dit laatste geen voorbode voor de uitkomst als onze algoritmes het tegen elkaar opnemen…
Een van de grote verschillen tussen de voorkeurAI-algoritmen aan de ene kant, en lerende algoritmen zoals de GeneticAI2 en QLearningAI, is dat de voorkeurAI-algoritmen nooit van tactiek wisselen. Zodra de QlearningAI dus de beste strategie heeft bepaald tegen een VoorkeurAI, zal hij die altijd blijven uitvoeren. Echter, als een lerend algoritme, zoals GeneticAI2, merkt dat een andere strategie beter is, past hij zich aan. Als een resultaat hiervan, zullen de q-waarden van QLearningAI zich zo aanpassen dat ook deze van strategie veranderd. Zoals je begrijpt is mijn voorspelling dat we ons de hele tijd aan elkaar zullen aanpassen. We gaan het meemaken, alleen nog niet in de volgende blog, want dan mengt ook Roelof zich in de strijd. Roelof, je hebt nog één maand!
Leren programmeren (duel)leren (deel 2)Mensen neigen nog vaak het idee te hebben dat de generatie die na hun komt, minder is dan hun eigen generatie. Misschien is dat toevallig voor jouw generatie wel waar, maar over het algemeen wordt de mensheid gemiddeld met de generaties, slimmer, sterker, sneller en ouder. Tenminste dat lijkt toch redelijk evident als je naar bijvoorbeeld wereldrecords kijkt, of naar het feit dat ik voor dit blog een computer zelf heb laten leren om boter-kaas-en-eieren te spelen, dat was een paar generaties geleden toch ondenkbaar. Dat de volgende generatie beter presteert dan de vorige is ook meteen hoe ik dat heb gedaan. In deel 2 van leren duelleren ga ik het hebben over een genetisch algoritme. De nieuwe bots kun je vinden op de volgende link: http://undercover.horse/tictactwo/
Maar eerst even een stukje administratie. Uit de reacties op mijn vorige blog begreep ik dat velen van jullie dachten dat Marlies deel 2 zou schrijven. Zoals jullie nu merken is dat niet het geval. Het oorspronkelijke plan was dat ik in dit deel iets meer uitleg zou geven over mijn algoritme, Marlies over haar algoritme, en dat ik dat dan aan elkaar zou knippen en plakken met hier en daar een stukje begeleidende tekst. De planning heeft alleen wat last gehad van mooi weer, vakantie en sociale verplichtingen, die niet in alle gevallen verplicht waren. Hierdoor is Marlies’ algoritme achterin de queue gekomen (dat is een briljant woordgrapje, maar je zult hem pas na Marlies’ blog snappen, maar geloof me, briljant). Dat betekent dat als je hier was voor het stukje van Marlies, dat ik je helaas danig (kijk ook een briljant woordgrapje, maar hier is dan weer geen voorkennis voor nodig) teleur moet stellen. Marlies schrijft deel 3, en dan zullen we dus de algoritmes op elkaar los laten, maar vandaag dus eerst deel 2: Survival of the fittest: kunstmatige selectie en intelligentie.
Charles Darwin, bij sommige misschien wel bekend, onderscheidt in zijn boek ‘on the Origin of Species’ (1859) twee soorten selectie die de evolutie aandrijven. Natuurlijke selectie, zoals het in de natuur gaat, en kunstmatige selectie zoals de mens dat doet bij bijvoorbeeld dure hondenrassen. Beide staven ze echter op dezelfde genetische principes. De ‘beste stukjes’ blijven over, en de ‘slechtste stukjes’ genetisch materiaal sterft langzaam af. Wat iets een goed stukje maakt is zeker in de biologie nogal een rekbaar begrip, maar heel kort door de bocht is dat hoe het werkt.
Dat idee wordt in de kunstmatige intelligentie geïmplementeerd middels een genetisch algoritme. Een genetisch algoritme werkt volgens volgend principe:
– Je begint met een zwik ‘bots’ met verschillende eigenschappen
– Je laat de bots los in de wereld waarin ze moeten overleven
– Je geeft de bots een score (de zogenaamde fitness score) aan de hand van hoe goed ze het doen
– Je laat de bots met een lage fitness score uitsterven, en die met een hoge fitness score laat je zichzelf voorplanten
– Bij het voortplanten laat je de bots muteren
– Zodra de huidige generatie voldoet aan je eisen stop je met het proces en de bots die je dan overhebt hebben de ‘juiste’ waardes.
Dat principe werkt niet helemaal geweldig met mijn boter-kaas-en-eieren spelletje, maar omdat volgens mij een genetisch algoritme een stuk makkelijk uit te leggen is dan bijvoorbeeld een neuraal netwerk, heb ik wat dichterlijke vrijheid toegepast en ga ik jullie laten zien hoe dat werkt.
Eerst kies ik een zwik aan mogelijke spel verlopen. Een mogelijk spelverloop is bijvoorbeeld [4, 8, 0, 6, 7, 2, 1, 3, 5]. In dit spelverloop kiest speler 1 als eerst vakje 4, vervolgens kiest speler 2 vakje 8, dan speler 1 vakje 0, etc. De volgende afbeelding laat zien welk vakje welke is:
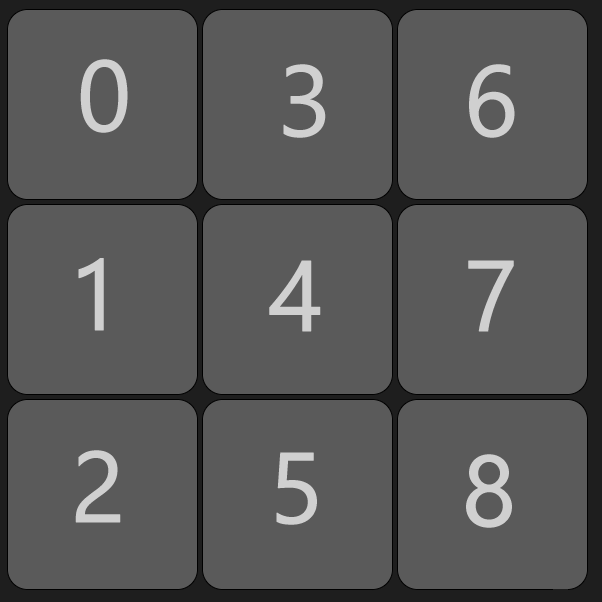
Boter-kaas-en-eieren experts zullen direct gezien hebben dat nadat speler 1 vakje 1 heeft gekozen hij 3 op een rij heeft (1,4,7) en dat de opties die daarna komen dus helemaal niet meer kunnen. Maar onze kunstmatige intelligentie is geen boter-kaas-en-eieren expert, sterker nog, hij kent de spelregels niet, zover hij ‘weet’ is dit een geldig spelverloop. De manier waarop ik de begin set maak is al volgt: Ik bereken alle mogelijkheden waarin de getallen 0 tot en met 8 in een volgorde kunnen staan (dat zijn er 362880) en dan geef ik elke combinatie een kans van 30 procent om in de begin set te komen. Vervolgens kopieer ik die set zodat ik 2 sets van ongeveer 100.000 spelverlopen heb. Eentje voor wanneer de AI begint, en eentje voor wanneer de tegenstander begint. Dit alles gebeurt voordat er een zet is gedaan, dus mogelijk dat je computer even bezig is als je een geneticAI speler kiest.
Vervolgens kijk ik naar het huidige spelverloop. Maak ik een verzameling van alle spelverlopen die voldoen aan het huidige spelverloop, en kies een willekeurige bot uit. Ik neem de volgende zet uit dat spelverloop en kies die. Als voorbeeld stel we zitten in het begin van het spel en de tegenstander heeft vakje 2 gekozen. Dan kijk ik in mijn verzameling met spelverlopen waar de tegenstander begint en daar zie ik 3 spelverlopen die beginnen met een 2:
[2, 8, 0, 6, 7, 4, 1, 3, 5] en [2, 4, 8, 0, 6, 7, 1, 3, 5] en [2, 8, 6, 0, 7, 4, 1, 3, 5]
Daar kies ik er willekeurig eentje van, bijvoorbeeld de eerste, de zet die ik dan ga zetten is de 8. De tegenstander is dan weer en kiest de 6. Ik ga opnieuw kijken welke spelverlopen ik nog heb. Het spel verloop is nu [2, 8, 6] waar ik net spelverloop 1 had gekozen kan dit nu niet meer, alleen spelverloop 3 is nu nog geldig, dus kies ik die, en zet ik de 0.
Dat proces herhaal ik tot dat het spelletje me vertelt dat het spel voorbij is. Zodra het spel afgelopen is, geef ik het huidige spelverloop een fitness waarde. 1 als ik heb gewonnen, 0 als ik gelijk heb gespeeld, en -1 als ik heb verloren.
Zo speel ik een aantal spelletjes, tot dat ik er een X-aantal heb gespeeld. Nu is het tijd voor een nieuwe generatie. Omdat er ik een heleboel spelverlopen nog niet heb gespeeld en die dus nog geen fitness score hebben laat ik die ongemoeid. Ik kijk alleen maar naar de spelverlopen met een negatieve fitness score, en ik wissel de laatste zet die ik heb gemaakt om met een willekeurige andere zet. Op basis van deze mutaties heb ik een nieuwe generatie. Dit blijf ik herhalen tot er geen spelverlopen meer zijn met een negatieve fitness waarde.
Iedereen die al naar de nieuwe bots heeft gekeken zal zijn opgevallen dat er 2 versies zijn. GeneticAI1 en geneticAI2, het verschil zit hem in hoe de mutatie werkt. In versie 1 wordt de zet verwisseld met een willekeurig andere zet. In versie 2 wordt er een lijst bijgehouden van spelverlopen met een positieve fitness score. Bij de mutatie wordt het spelverloop dat gemuteerd wordt vergeleken met een spelverloop met een positieve fitness code en wordt er alleen verwisseld met een zet die niet in het spelverloop met de positieve fitness score zit. Voorbeeldje? Voorbeeldje: Spelverloop waarbij de AI begint dat gemuteerd moet worden is: [4, 8, 0, 5, 6, 2, 1, 3, 7], spelverloop met een positieve fitness score: [4, 8, 0, 5, 2, 6, 1, 7, 3]. Het spelverloop heeft verloren na zet 6, zet 6 moet dus verwisseld worden met een andere zet. In versie 1 had dat elke zet kunnen zijn, en had je dus bijvoorbeeld spelverloop [6, 8, 0, 5, 4, 2, 1, 3, 7] kunnen krijgen. In versie 2 mag dat niet omdat de 4 in het winnende spelverloop op dezelfde plek zit, er mag daar alleen met de 2, 7 of de 3 gewisseld worden.
Nu hoor ik sommige van jullie denken: “Ik vraag me af hoe dat er in code uit ziet”, sommige andere hoor ik denken: “Dit is me al vaag en ingewikkeld genoeg, ik hoop niet dat hij ook nog code laat zien”, weer sommige andere: “Hmm ik heb honger, ik vraag me af of er nog iets lekkers in de kast ligt” en één iemand: ”Jemig wat een verhaal, moet ik ook zo’n enorm verhaal aan elkaar ratelen?“. Voor groep 4 heb ik een geruststellende mededeling: Nee Marlies, natuurlijk niet. Aan groep 3 zou ik adviseren gewoon even in de kast te kijken, het geheel is al complex genoeg voor op een volle maag, op een lege maag zou ik het iedereen afraden. Voor groep 2, geen zorgen als ik de code ga bespreken zitten we hier morgen nog. Voor groep 1 heb ik dan nog wel een klein beetje goed nieuws, je kunt de code zelf bekijken op respectievelijk http://undercover.horse/tictactwo/geneticAI.js en http://undercover.horse/tictactwo/geneticAI2.js en in versie zit nog wat extra commentaar zodat het hopelijk redelijk te volgen is. Ook zie je dan nog dat er een truc in zit voor als een spelverloop niet bestaat. Mocht je nou desondanks nog vragen, suggesties of opmerkingen er over hebben, mail me gerust.
Leuk zo’n kunstmatige intelligentie, maar werkt het überhaupt wel, en wat heb je er eigenlijk aan? Goede vragen, al zeg ik het en stel ik ze zelf. Nou heb ik het algoritme tijdens het schrijven van dit blog laten spelen tegen voorkeur2 en de voortgang een beetje bijgehouden, en dat ziet er als volgt uit:
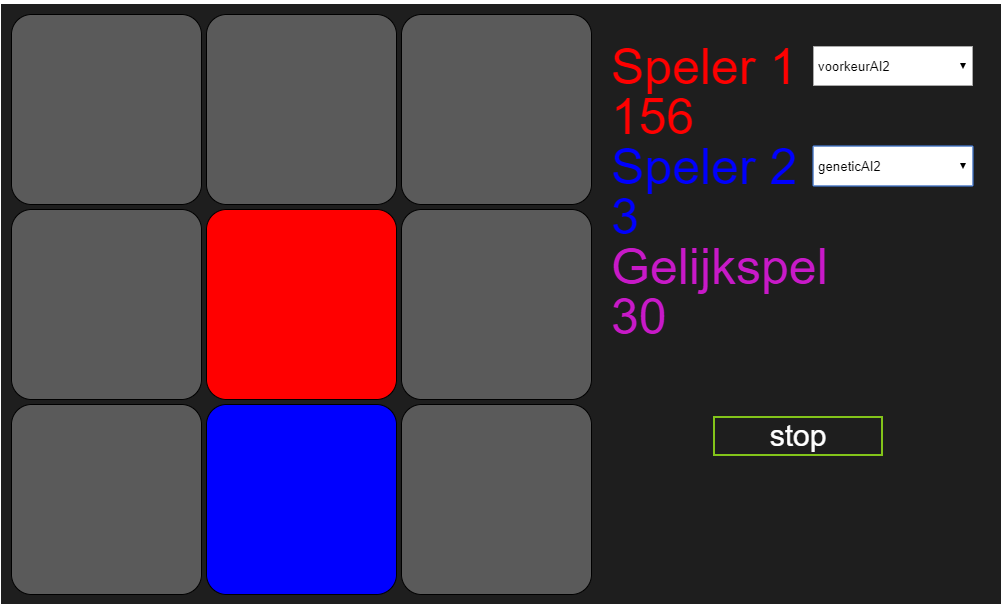
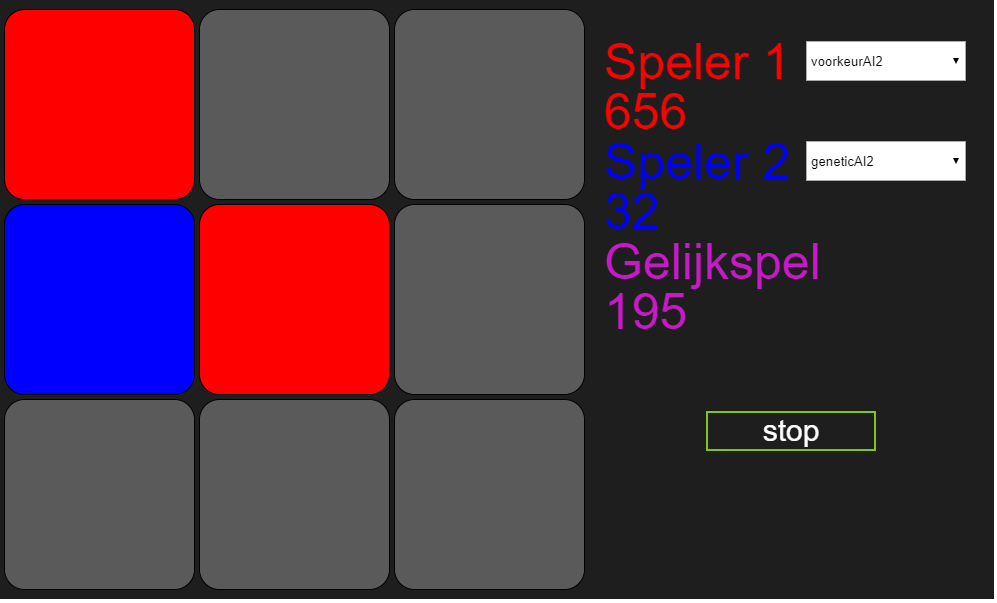

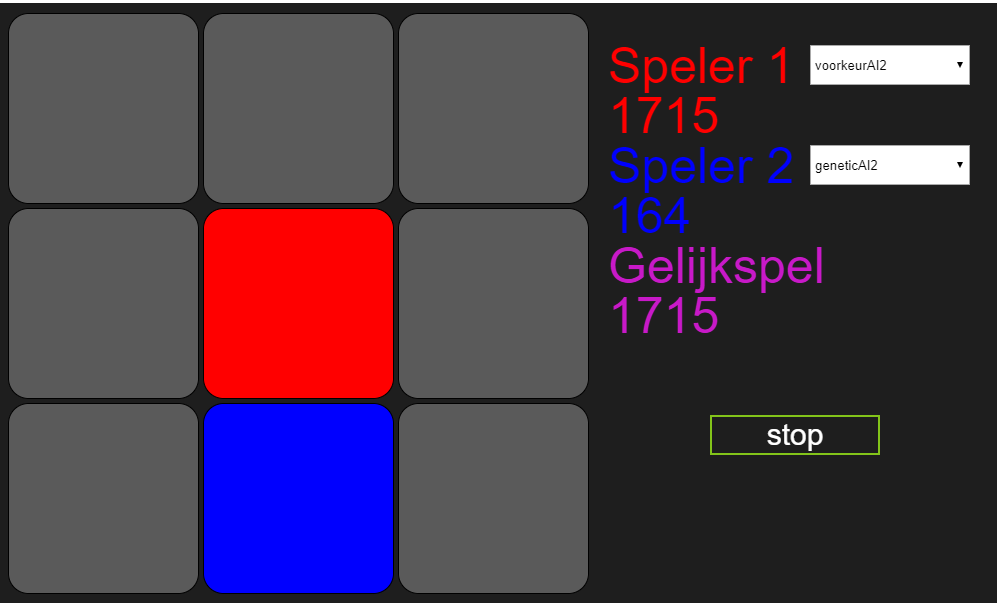
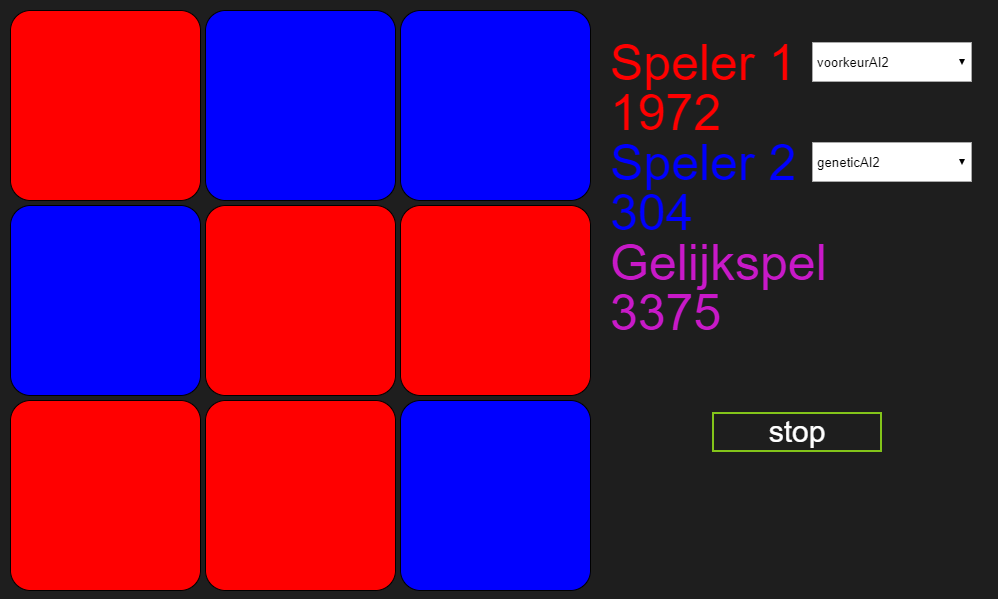
In het begin werden de meeste spelletjes verloren. Tegenover 50 verloren spelletjes stond 1 gewonnen spel en 10 gelijkspellen. Dat was te verwachten, het is een lerend algoritme, en leren kost tijd. Dat zie je ook mooi terug in de verdere verloop van de spellen, vooral in het aantal gelijkspellen. Voor wie het zich niet meer uit het vorige blog kan herinneren, voorkeurAI2 gebruikt altijd dezelfde volgorde van zetten, maar als hij een kans ziet om te winnen of een verlies te voorkomen doet hij dat. Het is voor het algoritme dus makkelijker om gelijk te spelen, en daar wordt hij ook niet voor bestraft, immers alleen spelverlopen met een negatieve fitness score worden gemuteerd. Maar het algoritme gaat ook steeds meer winnen, eerst was het tegenover 50 verloren spellen 1, op het laatst is het tegenover 7 verloren spellen 1. En uiteindelijk zal het algoritme vaker winnen dan verliezen
Het algoritme werkt dus, het leert, maar wat heeft dat voor zin? Zoals ik in het vorige blog al zei, voor dit specifieke voorbeeld niet zo veel. Het MiniMax-algoritme is snel genoeg om alle mogelijke zetten te voorzien en geeft dus altijd de beste zet terug. Toch wint het nooit van voorkeurAI2 omdat het ervan uitgaat dat voorkeurAI2 de best mogelijk zet gaat doen, terwijl deze dat niet altijd doet. Echter verliest MiniMax nooit, wat een duidelijk voordeel heeft. Maar ondanks dat het in dit voorbeeld niet heel zinvol is kan je er wel iets leuks aan zien. Ik heb het algoritme niks uitgelegd van de spelregels. Het enige wat het van tevoren ‘weet’ is dat je alleen maar een leeg vakje mag kiezen. Vervolgens vertel ik het zodra hij verloren, gewonnen of gelijk gespeeld heeft, maar meer niet. Maar het MiniMax-algoritme moest weten wat de waarde van een zet was, en dus moest weten wanneer er gewonnen zou worden, kent hij impliciet de spelregels. Ook voorkeurAI2 weet dat hij drie op een rij moet krijgen en zijn tegenstander niet. Je kunt een genetisch algoritme dan ook uitstekend gebruiken als je zelf het antwoord niet, of niet precies weet.
Dat is de grote kracht van kunstmatige intelligentie, het kan dingen leren die je zelf niet weet. Hoewel we nog niet bang hoeven te zijn voor filmscenario’s als Skynet uit Terminator of WarGames (Shall we play a game?), omdat kunstmatige intelligenties heel erg specifiek één ding leren, worden ze wel heel goed in dat ene specifieke ding. Er is daarom niemand meer die kan winnen van de beste kunstmatige intelligenties met schaken, jeopardy en sinds kort ook GO. Maar al die rekenkracht kan je natuurlijk ook voor praktischere dingen inzetten. Zo gaat er een bekende anekdote dat de Amerikaanse supermarktketen Target alle verkopen van klanten bij hield en een algoritme uit al die data vast liet stellen of de klant zwanger was of niet, en ze op basis daarvan kortingsbonnen stuurde voor baby artikelen. Op het laatst was het algoritme zo goed dat het in sommige gevallen eerder wist dat een vrouw zwanger was dan de vrouw zelf. Helaas blijkt deze anekdote niet waar, het algoritme is opgesteld door een statisticus en was niet zelflerend, en er gaan nog wel geruchten dat vaders er door Target coupons achter kwamen dat hun dochter zwanger was, maar in hoeverre dat waar is, is ook nog maar de vraag. Maar dit is wel iets dat prima met een KI-algoritme gedaan had kunnen worden.
Je zult steeds meer te maken krijgen met kunstmatige intelligenties, zelfs als je het zelf niet door hebt. Bijvoorbeeld de video’s die YouTube je aanraadt om te kijken, daarvan weten de mensen bij YouTube zelf niet op basis waarop dat gebeurt, dat zit allemaal verwerkt in een kunstmatig intelligent algoritme. Dat klinkt heel spannend, maar ik hoop dat ik met dit blog heb laten zien, dat het allemaal geen magie is. Tenminste volgens mij is het geen magie, ik weet natuurlijk niet wat mijn tegenstander in de strijd gaat gooien. Marlies?
Leren programmeren (duel)leren (deel 1)Nu ik inmiddels bezig ben met mijn 3de blog, is het misschien wel handig om uit te leggen wat het overkoepelende idee achter de blogs is. Trouwe lezers zullen inmiddels de gelijkenissen in de titel zijn opgevallen. Wees gerust, ik heb niet de illusie dat ik met een paar blogs van mijn lezers software developers kan maken. De titel is dan ook niet leren programmeren. Wat ik wel probeer, waarschijnlijk met afwisselend succes, is het idee van programmeren wat minder mysterieus te maken. In deel 2 van deze blog hoop ik daar nog een stapje bovenop te doen, en uit te leggen hoe kunstmatige intelligentie werkt. In een poging om dat geen saaie lap tekst te maken heb ik de hulp ingeroepen van één van mijn collega’s, Marlies. We gaan allebei een ‘kunstmatige intelligentie’ schrijven en die nemen het dan tegen elkaar op in een potje boter-kaas-en-eieren.
Voordat het echter zover is eerst deel 1: boter-kaas-en-eieren.
Voordat de bots voor deel 2 geschreven kunnen worden, is er het spel boter-kaas-en-eieren nodig waarmee de bots kunnen communiceren. Dat spel kun je hier spelen: tictactoe en als je wilt kan je de code voor het spelletje hier vinden: tictactoe.zip. Ik denk dat iedereen de regels van het spel wel kent, maar voor de vorm, en omdat het vrij simpel is, leg ik het nog een keer uit. Er zijn 2 spelers, elke speler mag om de beurt een vakje kiezen, dat is voor de rest van het spel zijn vakje. Wie het eerst 3 vakjes op een rij heeft (horizontaal, verticaal of diagonaal) wint. Zijn alle vakjes bezet en heeft geen van beide 3 op een rij, dan is het gelijkspel.
Op dit moment zijn er 6 bots die je kan kiezen: Human, RandomAI, VoorkeurAI, VoorkeurAI2, VoorkeurAI3 en MinmaxAI. Als je human kiest dan moet je zelf een vakje kiezen als je aan de beurt bent, als je een bot kies doet die een zet. Voordat ik omschrijf wat de bots doen en hoe ‘goed’ ze zijn is het het leukst als je zelf het spelletje speelt tegen de verschillende bots en kijkt of je de tactiek die ze gebruiken kan ontdekken, en welke vervolgens het succesvolst is. Ik wacht wel even.
…
…
…
…
Klaar? Ok, mijn verwachting is dat je van de RandomAI sowieso hebt kunnen winnen maar niet van MinmaxAI. Ik zal kort toelichten hoe de verschillende bots werken.
RandomAI
RandomAI is de simpelste van de bots, de bot krijgt het huidige speelbord binnen, kijkt welke vlakjes beschikbaar zijn en kiest er daarvan willekeurig eentje. Tegen de random bot is het makkelijk om expres te verliezen of te winnen, maar verdacht lastig om gelijk te spelen, terwijl als je een beetje goed bent in het spelletje dat tegen een menselijke tegenstander eigenlijk altijd de uitslag is.
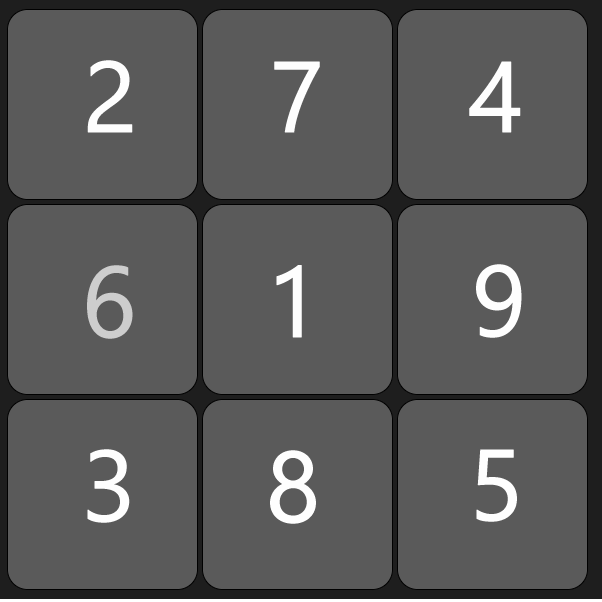
VoorkeurAI
VoorkeurAI is niet veel complexer dan RandomAI, deze bot heeft een vaste voorkeur voor welke vakjes hij wil hebben. Hij gaat deze voorkeur af en zodra er eentje beschikbaar is, claimt hij die.
Zijn voorkeur is als volgt:
Voor een simpele tactiek is dit helemaal nog niet zo slecht en je zal zien als je RandomAI tegen VoorkeurAI laat spelen dat VoorkeurAI meestal wint. Zelf zul je, als je dit weet echter makkelijk kunnen winnen, je kunt immers altijd de onderste rij (in de afbeelding dus 3,5,8) kiezen en winnen.
VoorkeurAI2
VoorkeurAI2 is al iets beter dan de andere 2 bots, hij heeft namelijk een win/verlies algoritme, als hij het spelletje kan winnen door een vlakje te kiezen, kiest hij deze. Zo niet, dan kijkt hij of de tegenstander kan winnen door een vlakje te kiezen, en zo ja dan kiest hij deze. Zo niet, dan valt hij terug op de tactiek van zijn kleine broertje en kiest hij de eerste lege op basis van dezelfde voorkeursvolgorde. Deze wint alles van VoorkeurAI en doet het een stuk beter tegen RandomAI. Je zult zien dat je ook van deze bot nog wel kunt winnen, maar je moet wel van te voren een goede tactiek bedenken!
VoorkeurAI3
VoorkeurAI3 is een beetje een instinker, als je er tegen gespeeld hebt, zal je waarschijnlijk het gevoel hebben dat hij iets beter is dan 2, ook al weet je niet precies waarom. In werkelijkheid is deze bot hetzelfde als VoorkeurAI2, met als enige verandering dat met een trucje hij er iets langer over doet om een oplossing uit de voorkeursvolgorde te halen.
Hier ga ik straks op verder, maar eerst laat ik Marlies de werking van de volgende bot uitleggen, die heeft zij namelijk gemaakt. Deze bot is de reden waarom we eigenlijk voor dit spelletje geen kunstmatige intelligentie nodig hebben. Er is namelijk een beter manier: Het minmax-algoritme.
MinmaxAI
De MinmaxAI bot gebruikt het minmax-algortime. Om dit algoritme te kunnen gebruiken, is er een aantal eigenschappen die een spelletje moet hebben. De eerste is dat jij wilt winnen, maar waarom speel je anders ook een spelletje, en dat je tegenstander ook wilt winnen, maar waarom speelt hij anders ook een spelletje, en dat de winst van de één betekent dat de ander verliest. Daarnaast is het nodig om ieder mogelijk vervolg van het spelletje te kunnen bepalen (dat is bij dit spel vrij makkelijk omdat het er niet veel zijn, alleen de eerste zet kost even wat tijd om uit te rekenen), en is het nodig om een waarde te kunnen hangen aan het einde van het spelletje.
Op het moment dat hij een zet moet doen, bedenkt het minmax-algoritme voor iedere mogelijke zet wat hiervan het gevolg is voor het vervolg van het spelletje. Op basis van dit vervolg, heeft een zet een bepaalde waarde. Zo heeft winst een waarde van +10, verlies een waarde van -10, en gelijkspel een waarde van 0. Daar waar jij probeert om deze waarde zo hoog mogelijk te maken, of dus te maximaliseren, probeert jouw tegenstander juist het omgekeerde te doen; oftewel te minimaliseren.
Op deze manier kan je ook voor een zet die er niet voor zorgt dat het spelletje is afgelopen een waarde bepalen. Als het spelletje nog niet is afgelopen, kan je namelijk beredeneren wat de tegenstander zal gaan doen, namelijk proberen om op een uitkomst met een zo laag mogelijke waarde uit te komen. Als hij echter het spelletje ook niet afmaakt, is het weer jouw beurt, en probeer jij juist weer op een zo hoog mogelijke waarde uit te komen. Als jij dan het spelletje niet afmaakt … enfin, je begrijpt het idee.
Echter missen we nu nog een essentieel onderdeel. Op dit moment heeft het winnen in de volgende zet dezelfde waarde als het winnen in een zet over vier beurten, namelijk +10. Daarnaast is de volgende beurt verliezen evenveel, of eigenlijk even weinig, waard als verliezen over vier beurten, namelijk -10. Tijd voor een voorbeeldje, als jij al twee vakjes op een rij hebt, is het niet zo handig om niet het derde vakje erbij te kiezen. Dat derde vakje kiezen, moet dus eigenlijk een hogere waarde hebben dan niet dat derde vakje kiezen. Ander voorbeeldje, als de tegenstander vakjes op een rij heeft, is het niet zo handig als je niet zelf het derde vakje kiest, anders wint hij namelijk zodra hij aan zet is. Oftewel, wel dat derde vakje kiezen moet een hogere, of minder lage, waarde hebben dan niet dat derde vakje kiezen.
Om hier rekening mee te houden, wordt de waarde van de uitkomst niet alleen bepaald door de uitkomst zelf, maar ook door het aantal beurten dat het nog kost om tot deze uitkomst te komen. Winnen in de volgende beurt krijgt dus een waarde van +10, terwijl winnen over vier beurten de waarde van +10 – 4 krijgt. Het omgekeerde is het geval voor verliezen. De volgende beurt verliezen is -10 punten, en pas over vier beurten verliezen heeft een waarde van -10 + 4. Hierdoor zal het algoritme winnen wanneer dat kan, en zorgen dat het niet de volgende beurt verliest.
Dankje Marlies voor deze heldere uitleg.
Deze tactiek maakt het minmax-algoritme onverslaanbaar. Immers hij berekent alle mogelijkheden, gaat uit van het scenario dat zijn tegenstander net zo goed is als hij en kiest dan de beste zet. Hoewel we hier een algoritme hebben dat altijd de beste zet doet, zal er niet zo snel iemand zijn die het kwalificeert als een intelligent algoritme. Maar als het maken van de slimste beslissing geen intelligentie is, wat dan wel?
Groot voordeel, daarover is geen algemene consensus, dus je mag zelf kiezen wat je intelligent noemt en als iemand het daar niet mee eens is, komt dat omdat hij/zij zelf niet intelligent genoeg is. Ik hoop dat je tegen voorkeurAI2 en 3 hebt gespeeld, en mijn voorspelling dat je het gevoel had dat 3 slimmer aanvoelde dan 2 uit is gekomen. Het illustreert namelijk iets mafs. Hoewel het niet zo is, lijkt de ene bot slimmer dan de andere. Dat kan door twee dingen komen:
1. De naam: Omdat voorkeurAI2 duidelijk slimmer is dan 1, zal 3 nog wel weer beter zijn. Dit is een hele menselijke vergissing waar veel reclamemakers graag gebruik van maken. Dit is ook de reden waarom we over een paar jaar scheermesjes hebben met acht mesjes, met namen als elemental fusion power daimond stealh razor deluxe hybrid. Want stom genoeg werkt het.
2. Het algoritme doet er langer over om een ‘moeilijke’ beslissing te nemen. Dit is iets wat je ziet gebeuren en je maakt een aanname waarom dat zo is: Het algoritme moet langer nadenken/rekenen over de keuze. Dat is echter niet zo, wat er in werkelijkheid gebeurt is dat het algoritme een willekeurig getal neemt tussen de 0 en 1, en als dat groter is dan 0,05 slaat hij een cyclus over. Het spelletje werkt met ongeveer 60 cycli per minuut, en dus duurt het even voordat hij daadwerkelijk zijn zet kiest.
Door ‘na te denken’ over de zet lijkt het algoritme menselijker, en wordt daarom sneller gezien als intelligent. In 1950 bedacht briljant wiskundige Alan Turing de Turing test. De Turing test werkt grofweg als volgt: Twee mensen voegen je toe op WhatsApp, geen van beide wil (video)bellen en je mag met beide 10 minuten appen. Na die 10 minuten moet je zeggen welk van deze 2 mensen ook echt een mens is en welke stiekem een computer. Als maar genoeg mensen het verschil niet kunnen onderscheiden tussen de mens en de computer dan is de computer intelligent.
Dat blijkt nog helemaal niet zo makkelijk, want als je iemand vraagt wat 23598 keer 123987 is en hij/zij komt direct met het goede antwoord, dan gaat al snel het vermoeden dat hij te goed kan rekenen en dus een computer is. Dus worden de bots trucjes aangeleerd, ze doen langer over rekensommen en maken bewust fouten. Maar dan ben je er nog lang niet, we zijn als mensen misschien niet zo goed in hoofdrekenen, het voeren van een conversatie kunnen we over het algemeen wel een stuk beter dan een computer. Er zijn veel projecten die deze uitdaging aangaan een voorbeeld is www.cleverbot.com. Chatten met cleverbot voelt als een discussie met mijn bijna 3-jarige nichtje, die als je vraagt of ze 2 handen heeft, heel stellig zegt: “Nee 3!”, terwijl ze evenveel vingers ophoudt als ze zondag jaren oud wordt. Nou klinkt dat niet zo bijzonder, maar dat betekent dat, volgens Turings redenatie, cleverbot de intelligentie heeft van een bijna 3-jarig meisje.
De Turing test wordt door veel mensen nog steeds gezien als de graadmeter voor intelligentie, maar hoewel we dat nog niet gehaald hebben vinden veel mensen het het doorstaan van de Turing niet genoeg om iets intelligent te noemen. Die vinden dat een intelligentie zou moeten kunnen functioneren in de echte wereld.
Nou wil ik niet voor Marlies praten, maar dat gaat mij wat te ver voor een blog. Wat wij gaan doen is een kleine doch zeer belangrijke subset van intelligentie, leren. We gaan allebei een algoritme schrijven dat na het spelen van potjes steeds beter wordt. Idealiter begint de bot zo goed als RandomAI en eindigt hij zo goed als MinmaxAI. Ik weet niet hoe het met jou zit Marlies, maar ik vrees dat ik hem niet zo goed ga krijgen als MinmaxAI, aan de andere kant verwacht ik wel dat hij kan winnen van mijn nichtje, ook al is ze inmiddels 3 als het algoritme af is. Kan het algoritme daarom beter leren dan mijn nichtje? Of beter nog, is het intelligent? Dat mag je zelf beslissen. Ik ben allang blij als het niet genadeloos verslagen wordt door dat van Marlies.
Wil je zelf ook een bot maken? In de zip-file staat een dummyAI, die doet nu nog helemaal niets, maar als je dummyAI.js aanpast kan je hem wel alles laten doen wat je wilt! Dus mocht je na het vorige blog de smaak van het programmeren te pakken hebben, maak van het duel een 3-strijd, laat je met de andere bots als voorbeeld inspireren en maak je eigen bot. Dan kan je in het volgend blog kijken hoe die zich verhoudt tegen die van ons! Mocht je een bot maken, zou ik het superleuk vinden als je je oplossing mailt. Het meest leer je immers van elkaar.
Rest me nog de competitie heel veel succes te wensen. Marlies, je hebt tot het volgende blog, succes, je tijd gaat nú in!
Hier komt de sidebar